题目内容
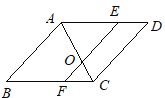
【题目】如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P点作PF⊥AD交BC的延长线于点F,交AC于点H.(1)∠APB的度数为_______°;(2)求证:△ABP≌△FBP;(3)求证:AH+BD=AB.

【答案】(1)135°,(2)见解析,(3)见解析
【解析】
(1)根据角平分线性质可得∠PAB+∠PBA=45°,即可解题.
(2)易得∠DPB=45°,可得∠BPF=135°,即可证得△ABP≌△FBP;
(3)由(2)可知∠F=∠BAD,AP=PF,AB=BF,即可求得∠F=∠CAD,可得AH=DF,即可解题.
(1)∵AD平分∠BAC,BE平分∠ABC,
∴∠PAB+∠PBA=![]() (∠ABC+∠BAC)=45°,
(∠ABC+∠BAC)=45°,
∴∠APB=180°-45°=135°.
(2)∵∠APB=135°.
∴∠DPB=45°,
∵PF⊥AD,
∴∠BPF=135°,
在△ABP和△FBP中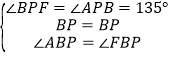
∴△ABP≌△FBP(ASA)
(3)∵△ABP≌△FBP,
∴∠F=∠BAD,AP=PF,AB=BF,
∵∠BAD=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中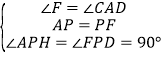
∴△APH≌△FPD(ASA)
∴AH=DF,
∵BF=DF+BD
∴AB=AH+BD

练习册系列答案
相关题目