Question

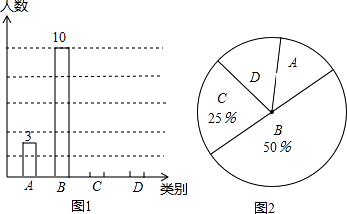
【题目】已知ABCD中，AD=2AB，F是BC的中点，作AE⊥CD，垂足E在线段CD上，连结EF、AF，下列结论：①2∠BAF=∠BAD；②EF=AF；③S△ABF≤S△AEF；④∠BFE=3∠CEF．中一定成立的是（　　）

A. ①②④ B. ①③ C. ②③④ D. ①②③④

Answer 1

【答案】D

【解析】因为F是BC的中点，所以F=FC，然后根据平行四边形的性质和AD=2AB，可得到BC=2AB=2CD，即BF=FC=AB，再根据“等边对等角”可得∠AFB=∠BAF，然后平行线的性质，可得∠AFB=∠FAB，即可得到2∠BAF=∠BAD，故①正确；

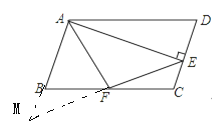
延长EF，交AB的延长线于M，由平行四边形的性质和中点的性质，可证明△MBF≌△ECF（ASA）然后根据全等三角形的性质和垂直的性质证得EF=AF，故②正确；

根据EF=FM可知S△EFC=S△AFM，所以可得S△ABF≤S△AEF，故③正确；

设∠FEA=x,则∠FAE=x，可得∠BAF=∠AFB=90°-x，进而求得∠EFA=180°-2x，则∠EFB=90°-x+180°-2x=270°-3x，再根据∠CFE=90°-x，可得∠BFE=3∠CEF，故④正确.

故选：D.