Question

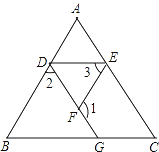
【题目】（本题满分10分）如图，在Rt△ABC中，∠A＝90°，BD平分∠ABC，M为边AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线AB于点F．试说明BD与MF的位置关系，并说明理由.

Answer 1

【答案】BD∥MF

【解析】试题分析：根据角平分线的定义与四边形的内角和定理求出∠ABD+∠AMF=90°，又∠AFM+∠AMF=90°，得到∠ABD=∠AFM，然后根据同位角相等，两直线平行可得BD∥MF．

试题解析：解： BD∥MF．理由如下：

∵∠A=90°，ME⊥BC，∴∠ABC+∠AME=360°﹣90°×2=180°．∵BD平分∠ABC，MF平分∠AME，∴∠ABD=∠ABC，∠AMF=∠AME，∴∠ABD+∠AMF=（∠ABC+∠AME）=90°．又∵∠AFM+∠AMF=90°，∴∠ABD=∠AFM，∴BD∥MF．