题目内容
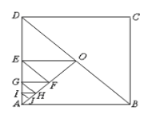
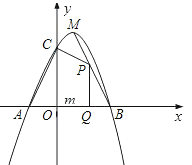
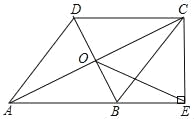
【题目】如图，直线
与
轴、
轴分别相交于
、
两点；分别过、两点作轴、轴的垂线相交于
点.
为
边上一动点．
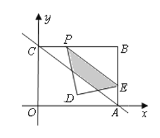
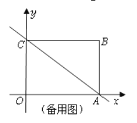
（1）求三角形
的面积；
（2）点从点出发沿着
以每秒1个单位长度的速度向点匀速运动，过点作
交
于
，设运动时间为
秒.用含的代数式表示
的面积
；
（3）在（2）的条件下点的运动过程中，将沿着
折叠（如图所示），点在平面内的落点为点
．当
与
重叠部分的面积等于
时，试求出点的横坐标．
【答案】（1）
的面积为24平方单位；（2）
；（3）当重叠部分的面积等于
时，
点的横坐标为 
或6．
【解析】
（1）结合图形，根据直线
与x轴、y轴分别相交于A、C两点即可求出点C的坐标，故可求出面积；
（2）先证明四边形OABC是矩形，根据性质得出BP的表达式，因为△BPE∽△BCA，求出BE表达式，进而求出△PBE的面积S．
（3）先求出D点在AC上的特殊位置时t的值，然后分两种情况求解．
（1）令=0，解得x=8
∴A（8,0）
令x=0，y=6
∴C（0，6）
∴三角形
的面积=
OA×OC=×8×6=24平方单位
（2）与
轴相交于点
∵
，
，
∴四边形
是矩形
∴
，
∴
∵
∴
∴
∴
∴
（3）设
、
与
分别相交于点
、
，得，
，
∵
∴
，
又∵
∴
∴
∴当点为
的中点时，
，点
恰好落在
上，
①当
时，
∵
∴
∴
∴
阴影
解得
，
（舍去）
∴点的横坐标为，
②当
时，
解得
，
（舍去）
∴点的横坐标为6
综上所述：当重叠部分的面积等于时，点的横坐标为 或6．
【题目】书籍是人类进步的阶梯．联合国教科文组织把每年的4月23日确定为“世界读书日”．某校为了了解该校学生一个学期阅读课外书籍的情况，在全校范围内随机对100名学生进行了问卷调查，根据调查的结果，绘制了统计图表的一部分：一个学期平均一天阅读课外书籍所有时间统计表
时间（分钟） | 20 | 40 | 60 | 80 | 100 | 120 |
人数（名） | 43 | 31 | 15 | 5 | 4 | 2 |
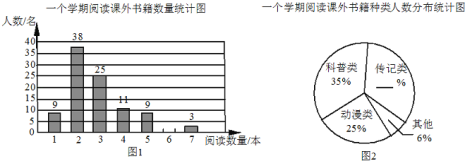
请你根据以上信息解答下列问题：
（1）补全图1、图2；
（2）这100名学生一个学期平均每人阅读课外书籍多少本？若该校共有4000名学生，请你估计这个学校学生一个学期阅读课外书籍共多少本？
（3）根据统计表，求一个学期平均一天阅读课外书籍所用时间的众数和中位数．
