题目内容
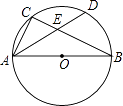
【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°. 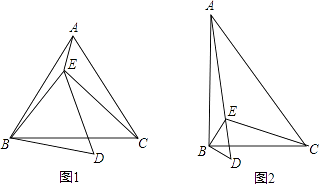
(1)当α=60°时(如图1), ①判断△ABC的形状,并说明理由;
②求证:BD= ![]() AE;
AE;
(2)当α=90°时(如图2),求 ![]() 的值.
的值.
【答案】
(1)解:①判断:△ABC是等边三角形.
理由:∵∠ABC=∠ACB=60°
∴∠BAC=180°﹣∠ABC﹣∠ACB=60°=∠ABC=∠ACB
∴△ABC是等边三角形
②证明:同理△EBD也是等边三角形
连接DC,
则AB=BC,BE=BD,∠ABE=60°﹣∠EBC=∠CBD
∴△ABE≌△CBD
∴AE=CD,∠AEB=∠CDB=150°
∴∠EDC=150°﹣∠BDE=90°∠CED=∠BEC﹣∠BED=90°﹣60°=30°
在Rt△EDC中 ![]() ,
,
∴ ![]()

(2)解:连接DC,
∵∠ABC=∠EBD=90°,∠ACB=∠EDB=60°
∴△ABC∽△EBD
∴ ![]()
又∵∠ABE=90°﹣∠EBC=∠CBD
∴△ABE∽△CBD,∠AEB=∠CDB=150°, ![]()
∴∠EDC=150°﹣∠BDE=90°∠CED=∠BEC﹣∠BED=90°﹣(90°﹣∠BDE)=60°
设BD=x在Rt△EBD中DE=2x,BE= ![]()
在Rt△EDC中CD= ![]()
∴ ![]() ,即
,即 ![]()

【解析】①由三角形ABC中有两个60°而求得它为等边三角形;②由△EBD也是等边三角形,连接DC,证得△ABE≌△CBD,在直角三角形中很容易证得结论.(2)连接DC,证得△ABC∽△EBD,设BD=x在Rt△EBD中DE=2x由相似比即得到比值.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目