题目内容
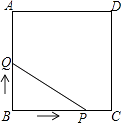
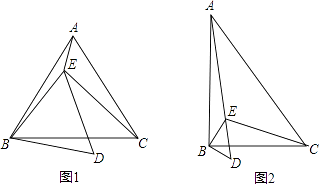
【题目】如图，直线l上摆放着两块大小相同的直角三角形△ABC和△ECD，∠ACB=∠DCE=90°，且BC=CE=3，AC=CD=4，将△ECD绕点C逆时针旋转到△E1CD1位置，且D1E1∥l ，则B、E1两点之间的距离为___________.
【答案】
【解析】过E1作E1F⊥BC，D1E1 与AC交于点O，如图：
∵D1E1∥l，∠DCE=90°，∴CO为△E1CD1的高，在△E1CD1中，BC=CE=CE1=3，AC=CD=CD1=4，
根据勾股定理得：D1E1=5，根据直角三角形面积公式
CE1CD1=
D1E1CO，解得：CO=
=E1F，
在Rt△CE1F中，利用勾股定理得：
，解得：CF=
，∴BF=BC-CF=3-
=
，
在Rt△BFE1中，利用勾股定理得：
，解得：
．
练习册系列答案
相关题目
【题目】一位射击运动员在10次射击训练中，命中靶的环数如图． 请你根据图表，完成下列问题：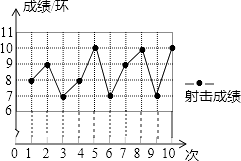
（1）补充完成下面成绩表单的填写：
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
（2）求该运动员这10次射击训练的平均成绩．
