Question

已知：如图所示，直线l的解析式为，并且与x轴、y轴分别交于点A、B.

（1）求A、B两点的坐标；

（2）一个圆心在坐标原点、半径为1的圆，以0.4个单位/秒的速度向x轴正方向运动，问在什么时刻与直线l相切；

（3）在题（2）中，若在圆开始运动的同时，一动点P从B点出发，沿射线BA方向以0.5个单位/秒的速度运动，设t秒时点P到动圆圆心的距离为s，求s与t的关系式；

（4）问在整个运动过程中，点P在动圆的圆面(圆上和圆内部)上，一共运动了多长时间？

 

Answer 1

【答案】

（1）（4，0），（0，－3）；（2）秒或秒；（3）；（4）秒.

【解析】

试题分析：（1）根据直线l的解析式为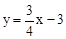直接求出A、B两点坐标即可；（2）当圆与直线相切时，分圆还直线l的左右侧两种情况讨论即可；（3）分和讨论即可；（4）设t秒时，圆心运动到点G，连接GP，先证明△AGP∽△AOB，且GP∥OB。从而根据点P进入和离开动圆的圆面的位置求出在整个运动的过程中，点P在动圆的圆面（圆上和圆的内部）上运动的时间.

试题解析：（1）∵直线l的解析式为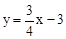，并且与x轴、y轴分别交于点A、B，

∴当y=0时，x=4；当x=0时，y=－3. ∴A、B两点的坐标分别为A（4，0），B（0，－3）.

（2）若动圆的圆心在C处时与直线l相切，设切点为D，

∵A（4，0）B（0，－3），∴AB=.

如图，连接CD，则CD⊥AD.

∵∠CAD=∠BAO，∠CDA=∠BOA=90⁰，∴Rt△ACD∽Rt△ABO. ∴.

∵CD=1，BO=3，AB=5，∴. ∴. ∴.

∵圆运动的速度为0.4个单位/每秒，∴t=（秒）.

根据对称性，圆还可能在直线l的右侧，与直线相切，

若动圆的圆心在E处时与直线l相切，设切点为F，此时，t=（秒）.

∴当圆运动秒或秒时圆与直线l相切.

（3）.

（4）如图，设t秒时，圆心运动到点G，连接GP，

∵动点P的速度是0.5个单位/秒，∴BP=0.5t，AP=5－0.5t.

∵动圆的速度是0.4个单位/秒，∴OG=0.4t，AP=4－0.4t.

∴. ∴.

∴△AGP∽△AOB，且GP∥OB. ∴GP⊥OA.

∴当GP=1（圆的半径）时，点P进入动圆的圆面.

∴，即. ∴.

∴点P经过AP的时间为（秒）.

根据对称性，点A的右边点P在动圆的圆面上还有秒.

∴在整个运动的过程中，点P在动圆的圆面（圆上和圆的内部）上一共运动了秒.

考点：1.一次函数综合题；2.动点和动圆问题；3.直线上点的坐标与方程的关系；4.勾股定理；5.相似三角形的判定和性质；6.平行的判定；7.点和圆的位置关系；8.分类思想的应用.