题目内容
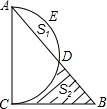 如图,以△ABC的边AC为直径的半圆交AB于D,三边长a,b,c能使二次函数y=
如图,以△ABC的边AC为直径的半圆交AB于D,三边长a,b,c能使二次函数y=| 1 |
| 2 |
| 1 |
| 2 |
(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1,阴影部分面积为S2,求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当b为何值时,(S2-S1)最大?
分析:(1)已知抛物线的顶点在x轴上,因此抛物线与x轴只有一个交点,令y=0,方程的△=0,由此即可证得三角形ABC为直角三角形,即可得出所求的结论.
(2)由于S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆因此只需求出三角形ABC和半圆的面积即可.根据题中给出的方程可求出a的值及BC的长,AC=b=2x,由此可求出三角形和半圆的面积,即可得出(S2-S1)与x的函数关系式.
(3)根据(2)得出的函数的性质即可求得(S2-S1)最大时对于的b的值.
(2)由于S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆因此只需求出三角形ABC和半圆的面积即可.根据题中给出的方程可求出a的值及BC的长,AC=b=2x,由此可求出三角形和半圆的面积,即可得出(S2-S1)与x的函数关系式.
(3)根据(2)得出的函数的性质即可求得(S2-S1)最大时对于的b的值.
解答:解:(1)因为二次函数y=
(a+c)x2-bx+
(c-a)的顶点在x轴上,
∴△=0,
即b2-4×
(a+c)×
(c-a)=0,
∴c2=a2+b2,
得∠ACB=90°,
或者从抛物线顶点的纵坐标为零求得
y=
=0,
可得c2=a2+b2;
(2)∵z2+z-20=0.
∴z1=-5,z2=4,
∵a>0,得a=4,
设b=AC=2x,有S△ABC=
AC•BC=4x,S半圆=
πx2,
∴S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆=-
x2+4x,
(3)S2-S1=-
(x-
)2+
,
∴当x=
,
即b=
时,(S2-S1)有最大值
.
| 1 |
| 2 |
| 1 |
| 2 |
∴△=0,
即b2-4×
| 1 |
| 2 |
| 1 |
| 2 |
∴c2=a2+b2,
得∠ACB=90°,
或者从抛物线顶点的纵坐标为零求得
y=
4×
| ||||
4×
|
可得c2=a2+b2;
(2)∵z2+z-20=0.
∴z1=-5,z2=4,
∵a>0,得a=4,
设b=AC=2x,有S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S2-S1=S△ABC-(S半圆-S1)-S1=S△ABC-S半圆=-
| π |
| 2 |
(3)S2-S1=-
| π |
| 2 |
| 4 |
| π |
| 8 |
| π |
∴当x=
| 4 |
| π |
即b=
| 8 |
| π |
| 8 |
| π |
点评:本题考查一元二次方程的解法,二次函数与一元二次方程的关系、勾股定理、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.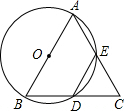 如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
 (2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.
(2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E. (2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.
(2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.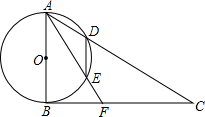 如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF
如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF