题目内容
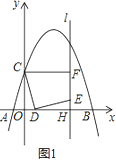
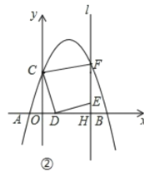
【题目】已知抛物线y=﹣![]() x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,且x1<0,x2>0,抛物线与y轴交于点C,OB=2OA.
(1)求抛物线解析式;
(2)已知直线y=![]() x+2与抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M1、N1,是否存在点P,同时满足如下两个条件:
x+2与抛物线相交于M、N两点,分别过M、N作x轴的垂线,垂足为M1、N1,是否存在点P,同时满足如下两个条件:
①P为抛物线上的点,且在直线MN上方;
②![]() :
:![]() =6:35
=6:35
若存在,则求点P横坐标t,若不存在,说明理由.

【答案】(1)y=﹣![]() x2+x+4 (2)存在,t=
x2+x+4 (2)存在,t=![]() 或t=﹣1
或t=﹣1
【解析】
(1)先求出x2=﹣2x1,再令y=0,用根与系数的关系得出x1+x2=﹣2(m+3),x1x2=﹣2(m2﹣12),即可得出结论;
(2)先求出M,N的坐标,进而求出梯形MM1N1N的面积,即可求出三角形PMN的面积,进而求出t的值,最后判断即可得出结论.
解:(1)∵A(x1,0)、B(x2,0)且x1<0,x2>0,
∴OA=﹣x1,OB=x2,
∵OB=2OA,
∴x2=﹣2x1,
∵抛物线y=﹣![]() x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,
x2﹣(m+3)x+m2﹣12与x轴交于A(x1,0)、B(x2,0)两点,
令y=0,
∴0=﹣![]() x2﹣(m+3)x+m2﹣12,
x2﹣(m+3)x+m2﹣12,
∴x2+2(m+3)x﹣2(m2﹣12)=0,
根据根与系数关系得,x1+x2=﹣2(m+3),x1x2=﹣2(m2﹣12),
∴﹣x1=﹣2(m+3),﹣2x12=﹣2(m2﹣12),
∴4(m+3)2=m2﹣12,∴m=﹣4,
∴抛物线解析式为y=﹣![]() x2+x+4;
x2+x+4;
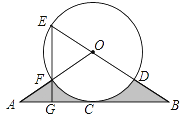
(2)如图,由(1)知,抛物线解析式为y=﹣![]() x2+x+4①,
x2+x+4①,

∴直线y=![]() x+2②与抛物线相交于M、N两点,
x+2②与抛物线相交于M、N两点,
联立①②解得,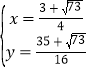 或
或 ,
,
∴N(![]() ,
,![]() ),M(
),M(![]() ,
,![]() ),
),
∴MM1=![]() ,NN1=
,NN1=![]() ,M1N1=
,M1N1=![]() ,
,
∴S梯形MM1N1N=![]() (MM1+NN1)×M1N1=
(MM1+NN1)×M1N1=![]() ,
,
∵![]() :
:![]() =6:35,
=6:35,
∴S△PMN=![]() ,
,
设P(t,﹣![]() t2+t+4),(
t2+t+4),(![]() <t<
<t<![]() ),
),
∴Q(t,![]() t+2),
t+2),
∴PQ=﹣![]() t2+t+4﹣
t2+t+4﹣![]() t﹣2=﹣
t﹣2=﹣![]() t2+
t2+![]() t+2,
t+2,
∴S△PMN=![]() PQM1N1=
PQM1N1=![]() (﹣
(﹣![]() t2+
t2+![]() t+2)×
t+2)×![]() =
=![]() ,
,
∴2t2﹣3t﹣5=0,
∴t=![]() 或t=﹣1,都符合题,
或t=﹣1,都符合题,
即:点P横坐标t=![]() 或t=﹣1.
或t=﹣1.
注:【利用估算的方法将t的范围缩放】
∵8.5<![]() <8.6,
<8.6,
∴﹣1.4<![]() <﹣1.3,
<﹣1.3,
2.875<![]() <2.9,
<2.9,
∵![]() <t<
<t<![]() ,
,
∴﹣1.3<t<2.875.

 阶梯计算系列答案
阶梯计算系列答案