题目内容
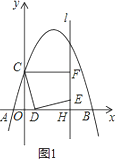
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于F.
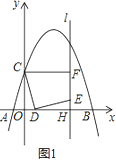
(1)求抛物线解析式;
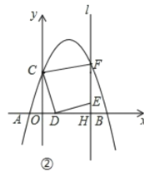
(2)如图②,当点F恰好在抛物线上时,求线段OD的长.
【答案】(1)y= ![]() x2+
x2+ ![]() x+3;(2)OD=1.
x+3;(2)OD=1.
【解析】
(1)利用待定系数法求得即可;
(2)根据C的纵坐标求得F的坐标,然后通过△OCD≌△HDE,得出DH=OC=3,即可求得OD的长
(1)解:如图1,
∵抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0)两点,
∴ ![]() ,
,
解得 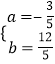 .
.
∴抛物线解析式为y= ![]() x2+
x2+ ![]() x+3
x+3
(2)解:如图2,∵点F恰好在抛物线上,C(0,3),

∴F的纵坐标为3,
把y=3代入y= ![]() x2+
x2+ ![]() x+3得,3=
x+3得,3= ![]() x2+
x2+ ![]() x+3;
x+3;
解得x=0或x=4,
∴F(4,3)
∴OH=4,
∵∠CDE=90°,
∴∠ODC+∠EDH=90°,
∴∠OCD=∠EDH,
在△OCD和△HDE中,
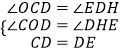 ,
,
∴△OCD≌△HDE(AAS),
∴DH=OC=3,
∴OD=4﹣3=1;

练习册系列答案
相关题目