题目内容
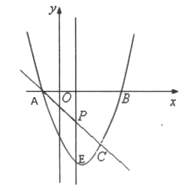
【题目】如图,已知二次函数y=x
－4x+3的图象交x轴于A，B两点（点A在点B的左侧）， 交y轴于点C.
（1）求直线BC的解析式；
（2）点D是在直线BC下方的抛物线上的一个动点，当△BCD的面积最大时，求D点坐标.
【答案】(1) y=-x+3；(2) （
,
）．
【解析】
试题（1）利用y=x2-4x+3的图象交x轴于A、B两点（点A在点B的左侧），抛物线y=x2-4x+3交y轴于点C，即可得出A，B，C点的坐标，将B，C点的坐标分别代入y=kx+b（k≠0），即可得出解析式；
（2）设过D点的直线与直线BC平行，且抛物线只有一个交点时，△BCD的面积最大．
试题解析：（1）设直线BC的解析式为：y=kx+b（k≠0）．
令x2-4x+3=0，
解得：x1=1，x2=3，
则A（1，0），B（3，0），C（0，3），
将B（3，0），C（0，3），代入y=kx+b（k≠0），得
，
解得：k=-1，b=3，
BC所在直线为：y=-x+3；
（2）设过D点的直线与直线BC平行，且抛物线只有一个交点时，△BCD的面积最大．
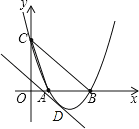
∵直线BC为y=-x+3，∴设过D点的直线为y=-x+b，
∴
，
∴x2-3x+3-b=0，
∴△=9-4（3-b）=0，
解得b=
，
∴
，
解得，
，
则点D的坐标为：（，-）．
【题目】近年来，“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注，为此，某校随机调查了n名学生对此问题的看法（看法分为三种：没有影响，影响不大，影响很大），并将调查结果 绘制成如下不完整的统计表和扇形统计图，根据统计图表提供的信息，解答下列问题：
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数（人） | 40 | 60 | m |
（1）求n的值；
（2）统计表中的m= ；
（3）估计该校1800名学生中认为“影响很大”的学生人数．
