题目内容
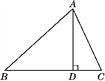
【题目】如图，在△ABC中，AD是BC边上的高，tanB＝cos∠DAC.
（1）求证：AC＝BD；
（2）若sin C＝
，BC＝12，求△ABC的面积．
【答案】（1）证明见解析；（2）△ABC的面积为48.
【解析】(1)∵AD是BC上的高，∴AD⊥BC．
∴∠ADB=90°，∠ADC=90°． …………………………………………1分
在Rt△ABD和Rt△ADC中，
∵
=
， 
=
…………………………………………3分
又已知
∴
=
．∴AC=BD． ………………………………4分
(2)在Rt△ADC中， 
，故可设AD=12k，AC=13k．
∴CD=
=5k．………………………………5分
∵BC=BD+CD，又AC=BD，
∴BC=13k+5k=18k ………………………………6分
由已知BC=12， ∴18k=12．∴k=
． ………………………………7分
∴AD=12k=12
=8． ……………………………8分
（1）在直角三角形中，表示
，根据它们相等，即可得出结论
（2）利用
和勾股定理表示出线段长，根据
，求出
长
练习册系列答案
相关题目
【题目】一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：
售价x（元/千克） | … | 50 | 60 | 70 | 80 | … |
销售量y（千克） | … | 100 | 90 | 80 | 70 | … |
（1）求y与x的函数关系式；
（2）该批发商若想获得4000元的利润，应将售价定为多少元？
（3）该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？
