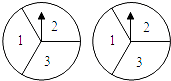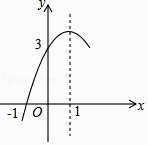题目内容
【题目】如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E,F.设CP=x,EF=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.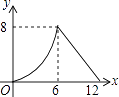
C.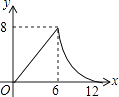
D.
【答案】D
【解析】解:AC与BD相交于O,
当点P在OC上时,如图1
∵四边形ABCD为平行四边形,
∴OC=OA= ![]() AC=6,
AC=6,
∵EF∥BD,
∴△CEF∽△CBD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴y= ![]() x(0≤x≤6);
x(0≤x≤6);
当点P在OA上时,如图2,
则AP=12﹣x,
∵EF∥BD,
∴△AEF∽△ABD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴y=﹣ ![]() x+16(6<x≤12),
x+16(6<x≤12),
∴y与x的函数关系的图象由正比例函数y= ![]() x(0≤x≤6)的图象和一次函数y=﹣
x(0≤x≤6)的图象和一次函数y=﹣ ![]() x+16(6<x≤12)组成.
x+16(6<x≤12)组成.
故选:D.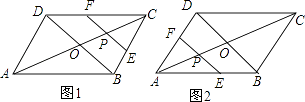
AC与BD相交于O,分类讨论:当点P在OC上时,根据平行四边形的性质得OC=OA= ![]() AC=6,利用EF∥BD得△CEF∽△CBD,根据相似比可得到y=
AC=6,利用EF∥BD得△CEF∽△CBD,根据相似比可得到y= ![]() x(0≤x≤6);
x(0≤x≤6);
当点P在OA上时,AP=12﹣x,由EF∥BD得△AEF∽△ABD,据相似比可得到y=﹣ ![]() x+16(6<x≤12),然后根据函数解析式对各选项分别进行判断.
x+16(6<x≤12),然后根据函数解析式对各选项分别进行判断.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】阅读可以增进人们的知识,也能陶冶人们的情操.我们要多阅读有营养的书.某校对学生的课外阅读时间进行了抽样调查,将收集的数据分成A,B,C,D,E五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
阅读时间分组统计表
组别 | 阅读时间x(h) | 人数 |
A | 0≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | b |
D | 30≤x<40 | 140 |
E | x≥40 | c |
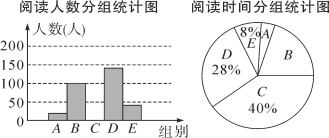
请结合以上信息解答下列问题:
(1)求a,b,c的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?