题目内容
如图,△ABC中,AB=AC,过BC上一点D作BC的垂线,交BA延长线与P,交AC于Q.
(1)判断△APQ的形状,并证明你的结论;
(2)若∠B=60°,AB=AC=2,设CD=x,四边形ABDQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围.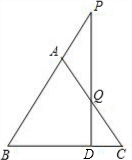
(1)判断△APQ的形状,并证明你的结论;
(2)若∠B=60°,AB=AC=2,设CD=x,四边形ABDQ的面积为y,求y与x之间的函数关系式,并写出x的取值范围.

(1)△APQ为等腰三角形,理由如下:
在△ABC中,AB=AC,
∴∠ABC=∠ACB.
∵P为BA延长线上一点,PD⊥BD交AC与Q点,
∴∠BDQ=∠BDP=90°.
∵∠QCD+∠DQC=90°,∠B+∠P=90°,∠ABC=∠ACB,
∴∠P=∠DQC,又∠AQP=∠DQC,
∴∠P=∠AQP,
∴AP=AQ,
∴△APQ为等腰三角形;
(2)∵∠B=60°,AB=AC=2,
∴△ABC为正三角形.
∵PD⊥BC,∠C=60°,
∴∠CQD=30°.
∴CQ=2DC=2x,
根据勾股定理 DQ=
=
x,
y=
×2×2sin60°-
x•
x=
-
x2(0<x<1),即y=
-
x2(0<x<1).
在△ABC中,AB=AC,
∴∠ABC=∠ACB.
∵P为BA延长线上一点,PD⊥BD交AC与Q点,
∴∠BDQ=∠BDP=90°.
∵∠QCD+∠DQC=90°,∠B+∠P=90°,∠ABC=∠ACB,
∴∠P=∠DQC,又∠AQP=∠DQC,
∴∠P=∠AQP,
∴AP=AQ,
∴△APQ为等腰三角形;
(2)∵∠B=60°,AB=AC=2,
∴△ABC为正三角形.
∵PD⊥BC,∠C=60°,
∴∠CQD=30°.
∴CQ=2DC=2x,
根据勾股定理 DQ=
| (2x)2-x2 |
| 3 |
y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目