题目内容
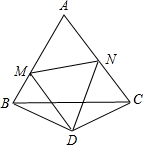
如图，已知△ABC是等边三角形，△BDC是顶角∠BDC=120°的等腰三角形，以D为顶点作一个60°角它的两边分别交AB于M，交AC于N，连接MN，求证：MN=BM+CN．
证明：如图，延长NC到E，使CE=BM，连接DE，
∵△ABC为等边三角形，△BCD为等腰三角形，且∠BDC=120°，
∴∠MBD=∠MBC+∠DBC=60°+30°=90°，
∠DCE=180°-∠ACD=180°-∠ABD=90°，
又∵BM=CE，BD=CD，
∴△CDE≌△BDM，
∴∠CDE=∠BDM，DE=DM，
∠NDE=∠NDC+∠CDE=∠NDC+∠BDM=∠BDC-∠MDN=120°-60°=60°，
∵在△DMN和△DEN中，
EDN=60°，
∴△DMN≌△DEN，
∴MN=NE=CE+CN=BM+CN．
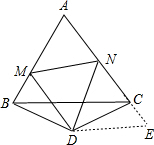
∵△ABC为等边三角形，△BCD为等腰三角形，且∠BDC=120°，
∴∠MBD=∠MBC+∠DBC=60°+30°=90°，
∠DCE=180°-∠ACD=180°-∠ABD=90°，
又∵BM=CE，BD=CD，
∴△CDE≌△BDM，
∴∠CDE=∠BDM，DE=DM，
∠NDE=∠NDC+∠CDE=∠NDC+∠BDM=∠BDC-∠MDN=120°-60°=60°，
∵在△DMN和△DEN中，
|
∴△DMN≌△DEN，
∴MN=NE=CE+CN=BM+CN．
练习册系列答案
目标测试系列答案
相关题目
