题目内容
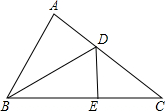
已知:如图,在△ABC中,D、E为边BC上两点,AB=AC,AD=AE.
求证:BD=CE.
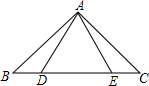
求证:BD=CE.

证明:作AF⊥BC,垂足为F,
因为AB=AC,AF⊥BC,
所以BF=CF
因为AD=AE,AF⊥BC,
所以DF=EF
所以BF-DF=CF-EF,
即BD=CE
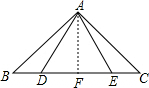
因为AB=AC,AF⊥BC,
所以BF=CF
因为AD=AE,AF⊥BC,
所以DF=EF
所以BF-DF=CF-EF,
即BD=CE


练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目