题目内容
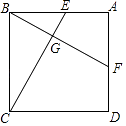
【题目】如图,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC;
(2)若AD=4,求AM的长.

【答案】(1)详见解析;(2)5
【解析】
(1)从平行线和中点这两个条件出发,延长AE、BC交于点N,易证△ADE≌△NCE,从而有AD=CN,只需证明AM=NM即可.
(2)设MC=x,则BM=4-x,由勾股定理与(1)的结论得出![]() ,解得x即可得出结果.
,解得x即可得出结果.
解:(1)证明:延长AE、BC交于点N,如图所示:
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAM,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
∴AM=MN,
在△ADE和△NCE中,

∴△ADE≌△NCE(AAS),
∴AD=NC,
∴AM=MN=NC+MC=AD+MC;
(2)解:∵四边形ABCD是正方形,
∴AB=BC=AD=4,∠B=90°,
设MC=x,则BM=4﹣x,
![]()
![]()
![]()
解得:x=1,
∴AM=5.


练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
【题目】青少年“心理健康”问题已经引起了社会的关注,某中学对全校850名学生进行了一次“心理健康”知识测试,并从中抽取了50名学生的成绩(得分取正整数,满分为100分)作为样本,列出下面的频数分布表(单位:分)
成绩 | 50.5≤x<60.5 | 60.5≤x<70.5 | 70.5≤x<80.5 | 80.5≤x<90.5 | 90.5≤x<100.5 |
频数 | 2 | 8 | 10 | 16 | 14 |
(1)组距是 ,组数是 .
(2)成绩在60.5≤x<80.5范围的频数是 .
(3)画出频数分布直方图.
(4)若成绩在80分以上(不含80分)为优秀,试估计该校成绩优秀的有多少人?