题目内容
【题目】如图,在 ![]() 中,
中, ![]() ,AB=BC,A,B的坐标分别为
,AB=BC,A,B的坐标分别为 ![]() ,将
,将 ![]() 绕点P旋转
绕点P旋转 ![]() 后得到
后得到 ![]() ,其中点B的对应点
,其中点B的对应点 ![]() 的坐标为
的坐标为 ![]() .
.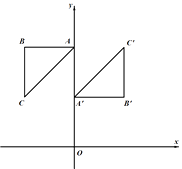
(1)求出点C的坐标;
(2)求点P的坐标,并求出点C的对应点 ![]() 的坐标.
的坐标.
【答案】
(1)解:∵A、B 的坐标分别为(0,4)(-2,4) ,
∴AB=2,
∴BC=AB=2,
∵∠B=90°,AB∥x轴,
∴BC⊥x轴,
所以点C的坐标为(-2,2)
(2)解:∵B点的对应点为B’点,
∴点P为BB’的中点,
∴点P的横坐标为: ![]() =0,纵坐标为:
=0,纵坐标为: ![]() =3,
=3,
即P(0,3);
设C’(x,y),
根据旋转的性质可知:点P为CC’的中点,
∴ ![]() =0,
=0, ![]() =3,
=3,
解得:x=2,y=4,
∴C’(2,4).
【解析】直接利用平移的性质得出平移规律即可;利用旋转的性质得出对应点位置进而得出答案,
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
相关题目