题目内容
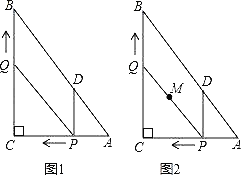
【题目】如图1，抛物线y=ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．
（1）求a的值和直线AB的函数表达式；
（2）设△PMN的周长为C1 ， △AEN的周长为C2 ， 若 
= 
，求m的值；
（3）如图2，在（2）条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α（0°＜α＜90°），连接E′A、E′B，求E′A+ 
E′B的最小值．
【答案】
（1）
解：令y=0，则ax2+（a+3）x+3=0，
∴（x+1）（ax+3）=0，
∴x=﹣1或﹣ 
，
∵抛物线y=ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），
∴﹣ =4，
∴a=﹣ 
．
∵A（4，0），B（0，3），
设直线AB解析式为y=kx+b，则 
，
解得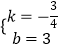 
，
∴直线AB解析式为y=﹣ x+3
（2）
解：如图1中，
∵PM⊥AB，PE⊥OA，
∴∠PMN=∠AEN，∵∠PNM=∠ANE，
∴△PNM∽△ANE，
∴ 
= 
，
∵NE∥OB，
∴ 
= 
，
∴AN= 
（4﹣m），
∵抛物线解析式为y=﹣ x2+ 
x+3，
∴PN=﹣ m2+ m+3﹣（﹣ m+3）=﹣ m2+3m，
∴ 
= ，
解得m=2．
（3）
解：如图2中，在y轴上 取一点M使得OM= 
，
∵OE′=2，OMOB= ×3=4，
∴OE′2=OMOB，
∴ 
= 
，∵∠BOE′=∠MOE′，
∴△MOE′∽△E′OB，
∴ 
= 
= 
，
∴ME′= BE′，
∴AE′+ BE′=AE′+E′M=AM′，
此时AE′+ BE′最小，最小值=AM= 
= 
【解析】（1）令y=0，求出抛物线与x轴交点，列出方程即可求出a，根据待定系数法可以确定直线AB解析式．（2）由△PNM∽△ANE，推出 = ，列出方程即可解决问题．（3）在y轴上 取一点M使得OM= ，构造相似三角形，可以证明AM就是E′A+ E′B的最小值．本题考查相似三角形的判定和性质、待定系数法、最小值问题等知识，解题的关键是构造相似三角形，找到线段AM就是E′A+ E′B的最小值，属于中考压轴题．
【考点精析】利用二次函数的最值和相似三角形的判定与性质对题目进行判断即可得到答案，需要熟知如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
