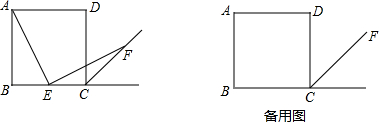题目内容
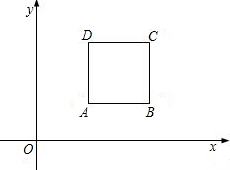 如图,四边形ABCD是正方形,已知A(5,4),B(10,4):
如图,四边形ABCD是正方形,已知A(5,4),B(10,4):
(1)求点C、D的坐标;
(2)若一次函数y=kx+3(k≠0)的图象过C点,求k的值;
(3)在(2)的条件下,①若将直线l:y=kx+3向下平移a个单位,将正方形分为上下两部分的面积比为7:3,试求出a的值;②若将直线l:y=kx+3平移后与以A为圆心,AC为半径的圆相切,直接写出平移后的直线的解析式.
解:(1)已知A(5,4),B(10,4),则AB=5,即正方形的边长为5;
故C(10,9),D(5,9).
(2)将点C(10,9)代入直线l的解析式中,
得:10k+3=9,
即k= .
.
(3)①设平移后的直线l′:y= x+3-a(a>0);
x+3-a(a>0);
1)当直线l′与线段AD、BC相交时,
设交点分别为M、N,则M(5,6-a),N(10,9-a);
故MA=2-a,NB=5-a;
由题意得:S梯形MABN= (2-a+5-a)×5=25×
(2-a+5-a)×5=25×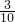 ,
,
解得a=2;
2)当直线l′与线段AB、BC相交时,同1)可求得a=2;
综上可知:a=2.
②设平移后的直线l″:y= x+3+b,即
x+3+b,即 x-y+3+b=0;
x-y+3+b=0;
易知AC=5 ,A(5,4);
,A(5,4);
由题意得: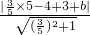 =5
=5 ;
;
解得b=±2 -2;
-2;
故平移后的直线解析式为:y= 或y=
或y=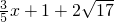 .
.
分析:(1)根据A、B的坐标,即可得到正方形的边长,进而可根据A、B的坐标,得到C、D的坐标.
(2)将C点坐标代入所求的直线解析式中,即可求得k的值.
(3)①此题要分两种情况进行讨论:
1)平移后的直线l与线段AD、BC相交,可先设出平移后的直线l解析式,将A、B横坐标分别代入该直线的解析式中,即可得到此直线与AD和BC的交点(设为M、N),进而可求出梯形MABN(或△ABN)的面积,由于直线将梯形分成7:3的两部分,那么梯形MABN的面积为:25×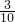 ,可据此列出关于a的等量关系式,进而求得a的值;
,可据此列出关于a的等量关系式,进而求得a的值;
2)平移后的直线l于线段AB、BC相交,解法同1).
②首先设出平移后的直线解析式,若此直线与⊙A相切,易得⊙A的半径为5 ,则点A到此直线的距离为5
,则点A到此直线的距离为5 ,利用点到直线的距离公式,即可求出该平移的距离,由此得解.
,利用点到直线的距离公式,即可求出该平移的距离,由此得解.
点评:此题主要考查了正方形的性质、图形面积的求法、函数解析式的确定、函数图象的平移、直线与圆的位置关系等重要知识,难度较大.
故C(10,9),D(5,9).
(2)将点C(10,9)代入直线l的解析式中,
得:10k+3=9,
即k=
 .
.(3)①设平移后的直线l′:y=
 x+3-a(a>0);
x+3-a(a>0);1)当直线l′与线段AD、BC相交时,
设交点分别为M、N,则M(5,6-a),N(10,9-a);
故MA=2-a,NB=5-a;
由题意得:S梯形MABN=
 (2-a+5-a)×5=25×
(2-a+5-a)×5=25×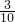 ,
,解得a=2;
2)当直线l′与线段AB、BC相交时,同1)可求得a=2;
综上可知:a=2.
②设平移后的直线l″:y=
 x+3+b,即
x+3+b,即 x-y+3+b=0;
x-y+3+b=0;易知AC=5
 ,A(5,4);
,A(5,4);由题意得:
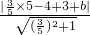 =5
=5 ;
;解得b=±2
 -2;
-2;故平移后的直线解析式为:y=
 或y=
或y=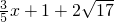 .
.分析:(1)根据A、B的坐标,即可得到正方形的边长,进而可根据A、B的坐标,得到C、D的坐标.
(2)将C点坐标代入所求的直线解析式中,即可求得k的值.
(3)①此题要分两种情况进行讨论:
1)平移后的直线l与线段AD、BC相交,可先设出平移后的直线l解析式,将A、B横坐标分别代入该直线的解析式中,即可得到此直线与AD和BC的交点(设为M、N),进而可求出梯形MABN(或△ABN)的面积,由于直线将梯形分成7:3的两部分,那么梯形MABN的面积为:25×
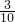 ,可据此列出关于a的等量关系式,进而求得a的值;
,可据此列出关于a的等量关系式,进而求得a的值;2)平移后的直线l于线段AB、BC相交,解法同1).
②首先设出平移后的直线解析式,若此直线与⊙A相切,易得⊙A的半径为5
 ,则点A到此直线的距离为5
,则点A到此直线的距离为5 ,利用点到直线的距离公式,即可求出该平移的距离,由此得解.
,利用点到直线的距离公式,即可求出该平移的距离,由此得解.点评:此题主要考查了正方形的性质、图形面积的求法、函数解析式的确定、函数图象的平移、直线与圆的位置关系等重要知识,难度较大.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.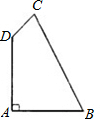 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.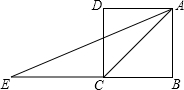 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.