题目内容
如图,已知抛物线y=ax2+bx+c的顶点为P(1,-2),且经过点A(-3,6),并与x轴交于点B和C.
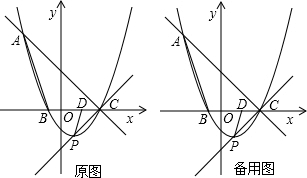
(1)求这个二次函数的解析式,并求出点C坐标及∠ACB的大小;
(2)设D为线段OC上一点,满足∠DPC=∠BAC,求D的坐标;
(3)在x轴上,是否存在点M,使得以M为圆心的圆能与直线AC、直线PC及y轴都相切?如果存在,求出点M的坐标;若不存在,请说明理由.

(1)求这个二次函数的解析式,并求出点C坐标及∠ACB的大小;
(2)设D为线段OC上一点,满足∠DPC=∠BAC,求D的坐标;
(3)在x轴上,是否存在点M,使得以M为圆心的圆能与直线AC、直线PC及y轴都相切?如果存在,求出点M的坐标;若不存在,请说明理由.
(1)∵顶点为P(1,-2),
∴设二次函数顶点式解析式为y=a(x-1)2-2,
把点A(-3,6)代入得,a(-3-1)2-2=6,
解得a=
,
所以,二次函数解析式为y=
(x-1)2-2=
x2-x-
,
即y=
x2-x-
;
令y=0,则
x2-x-
=0,
整理得,x2-2x-3=0,
解得x1=-1,x2=3,
∴点C坐标为(3,0);
∵A(-3,6),C(3,0),
∴tan∠ACB=
=1,
∴∠ACB=45°;
(2)∵点P(1,-2),C(3,0),
∴tan∠PCD=
=1,
∴∠PCD=45°,
∴∠PCD=∠ACB,
又∵∠DPC=∠BAC,
∴△DPC∽△BAC,
∴
=
,
∵AC=
=6
,PC=
=2
,BC=3-(-1)=4,
∴
=
,
解得DC=
,
∴OD=OC-DC=3-
=
,
∴点D的坐标为(
,0);
(3)如图,①点M在线段OC上时,设AC切⊙O于H1,连接MH1,
∵⊙M与直线AC相切,
∴MH1⊥AC,
∵∠ACB=45°,
∴OC=OM+CM=OM+
OM=3,
解得OM=
=3
-3;
此时,点M(3
-3,0);
②点M在射线OB上时,设AC切⊙O于H2,连接MH2,
∵⊙M与直线AC相切,
∴MH2⊥AC,
∵∠ACB=45°,
∴OC=CM-OM=
OM-OM=3,
解得OM=
=3
+3.
此时,点M(-3
-3,0).
∴设二次函数顶点式解析式为y=a(x-1)2-2,
把点A(-3,6)代入得,a(-3-1)2-2=6,
解得a=
| 1 |
| 2 |
所以,二次函数解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
即y=
| 1 |
| 2 |
| 3 |
| 2 |
令y=0,则
| 1 |
| 2 |
| 3 |
| 2 |
整理得,x2-2x-3=0,
解得x1=-1,x2=3,
∴点C坐标为(3,0);
∵A(-3,6),C(3,0),
∴tan∠ACB=
| 6 |
| 3+3 |
∴∠ACB=45°;
(2)∵点P(1,-2),C(3,0),
∴tan∠PCD=
| 2 |
| 3-1 |
∴∠PCD=45°,
∴∠PCD=∠ACB,
又∵∠DPC=∠BAC,
∴△DPC∽△BAC,
∴
| DC |
| BC |
| PC |
| AC |
∵AC=
| 62+(3+3)2 |
| 2 |
| 22+(3-1)2 |
| 2 |
∴
| DC |
| 4 |
2
| ||
6
|
解得DC=
| 4 |
| 3 |
∴OD=OC-DC=3-
| 4 |
| 3 |
| 5 |
| 3 |
∴点D的坐标为(
| 5 |
| 3 |
(3)如图,①点M在线段OC上时,设AC切⊙O于H1,连接MH1,
∵⊙M与直线AC相切,

∴MH1⊥AC,
∵∠ACB=45°,
∴OC=OM+CM=OM+
| 2 |
解得OM=
| 3 | ||
|
| 2 |
此时,点M(3
| 2 |
②点M在射线OB上时,设AC切⊙O于H2,连接MH2,
∵⊙M与直线AC相切,
∴MH2⊥AC,
∵∠ACB=45°,
∴OC=CM-OM=
| 2 |
解得OM=
| 3 | ||
|
| 2 |
此时,点M(-3
| 2 |

练习册系列答案
相关题目



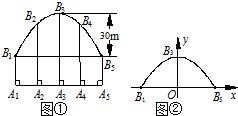
 的矩形花圃.
的矩形花圃.