题目内容
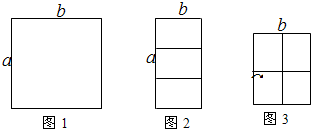
在一大片空地上有一堵墙(线段AB),现有铁栏杆40m,准备充分利用这堵墙建造一个封闭 的矩形花圃.
的矩形花圃.
(1)如果墙足够长,那么应如何设计可使矩形花圃的面积最大?
(2)如果墙AB=8m,那么又要如何设计可使矩形花圃的面积最大?
 的矩形花圃.
的矩形花圃.(1)如果墙足够长,那么应如何设计可使矩形花圃的面积最大?
(2)如果墙AB=8m,那么又要如何设计可使矩形花圃的面积最大?
(1)设DE=x,那么面积S=x(20-
)
=-
+20x=-
(x-20)2+200
∴当DE=20m时,矩形的面积最大是200m2

(2)讨论①设DE=x,那么面积S=x(20-
)(0<x≤8)
=-
(x-20)2+200
∴当DE=8m时,矩形的面积最大是128m2.
②延长AB至点F,作如图所示的矩形花圃
设BF=x,那么AF=x+8,AD=16-x
那么矩形的面积S=(x+8)(16-x)
=-x2+8x+128
=-(x-4)2+144
∴当x=4时,面积S的最大值是144.
∴按第二种方法围建的矩形花圃面积最大是144m2
| x |
| 2 |
=-
| x2 |
| 2 |
| 1 |
| 2 |
∴当DE=20m时,矩形的面积最大是200m2

(2)讨论①设DE=x,那么面积S=x(20-
| x |
| 2 |
=-
| 1 |
| 2 |
∴当DE=8m时,矩形的面积最大是128m2.
②延长AB至点F,作如图所示的矩形花圃
设BF=x,那么AF=x+8,AD=16-x
那么矩形的面积S=(x+8)(16-x)
=-x2+8x+128
=-(x-4)2+144
∴当x=4时,面积S的最大值是144.
∴按第二种方法围建的矩形花圃面积最大是144m2

练习册系列答案
相关题目
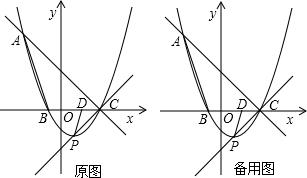
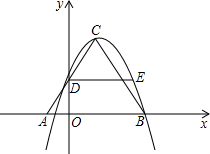

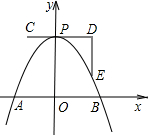

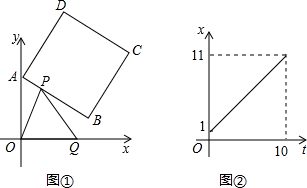 能,写出所有符合条件的t的值;若不能,请说明理由.
能,写出所有符合条件的t的值;若不能,请说明理由.