Question

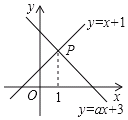
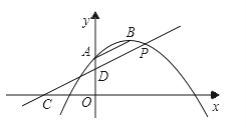
【题目】已知抛物线y=ax2﹣4ax+c经过点A（0，2），顶点B的纵坐标为3．将直线AB向下平移，与x轴、y轴分别交于点C、D，与抛物线的一个交点为P，若D是线段CP的中点，则点P的坐标为________．

Answer 1

【答案】（，）

【解析】

试题首先求出顶点坐标，利用待定的系数法求得物线的解析式；求出直线AB，进一步得到直线PC的解析式，由此联立一元二次方程求得结果．

试题解析：抛物线y=ax2-4ax+b的对称轴是x=，顶点坐标为B（2，3），且经过A（0，2），

代入函数解析式得，

解得，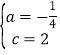

所以函数解析式为y＝x2+x+2；

如图，

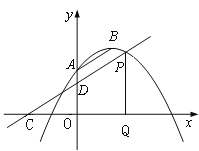
设P点坐标为（x，x2+x+2），过点P作PQ⊥x轴，垂足为Q，可得到△COD∽△CQP，

，又因为，所以

因此D点坐标为（0，x2+x+1），

经过A、B两点直线AB的解析式为y=x+2，

因此直线CP的解析式为y=x+（-x2+x+1）=-x2+x+1，与抛物线联立方程得，

-x2+x+2=-x2+x+1，解得x=，（负舍去）

代入抛物线解析式可得y=，

因此P点坐标为P(，)．

考点: 二次函数综合题．