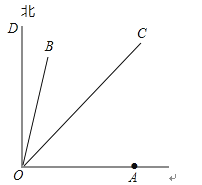题目内容
【题目】已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
(1)求m的值及抛物线E2所表示的二次函数的表达式;
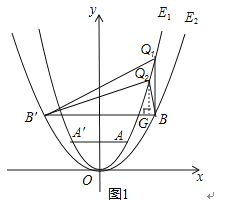
(2)如图1,在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
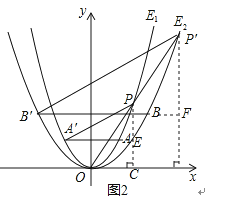
(3)如图2,P为第一象限内的抛物线E1上与点A不重合的一点,连接OP并延长与抛物线E2相交于点P′,求△PAA′与△P′BB′的面积之比.
【答案】
(1)
解:∵抛物线E1经过点A(1,m),
∴m=12=1.
∵抛物线E2的顶点在原点,可设它对应的函数表达式为y=ax2(a≠0),
又∵点B(2,2)在抛物线E2上,
∴2=a×22,
解得:a=![]() ,
,
∴抛物线E2所对应的二次函数表达式为y=![]() x2.
x2.
(2)
解:如图1,假设在第一象限内,抛物线E1上存在点Q,使得△QBB′为直角三角形,
由图象可知直角顶点只能为点B或点Q.
①当点B为直角顶点时,过B作QB⊥BB′交抛物线E1于Q,
则点Q与B的横坐标相等且为2,将x=2代入y=x2得y=4,
∴点Q的坐标为(2,4).
②当点Q为直角顶点时,则有QB′2+QB2=B′B2,过点Q作GQ⊥BB′于G,
设点Q的坐标为(t,t2)(t>0),
则有(t+2)2+(t2﹣2)2+(2﹣t)2+(t2﹣2)2=4,
整理得:t4﹣3t2=0,
∵t>0,∴t2﹣3=0,解得t1=![]() ,t2=
,t2=![]() (舍去),
(舍去),
∴点Q的坐标为(![]() ,3),
,3),
综合①②,存在符合条件的点Q坐标为(2,4)与(![]() ,3)
,3)
(3)
解:如图2,过点P作PC⊥x轴,垂足为点C,PC交直线AA′于点E,
过点P′作P′D⊥x轴,垂足为点D,P′D交直线BB′于点F,
依题意可设P(c,c2)、P′(d,![]() d2) (c>0,c≠q),
d2) (c>0,c≠q),
∵tan∠POC=tan∠P′OD,
∴![]() ,
,
∴d=2c.
∵AA′=2,BB′=4,
∴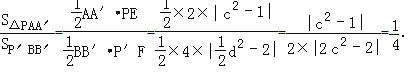
【解析】(1)直接将(2,2)代入函数解析式进而求出a的值;
(2)由题意可得,在第一象限内,抛物线E1上存在点Q,使得△QBB′为直角三角形,由图象可知直角顶点只能为点B或点Q,分别利用当点B为直角顶点时以及当点Q为直角顶点时求出Q点坐标即可;
(3)首先设P(c,c2)、P′(d,![]() d2),进而得出c与d的关系,再表示出△PAA′与△P′BB′的面积进而得出答案.
d2),进而得出c与d的关系,再表示出△PAA′与△P′BB′的面积进而得出答案.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系和二次函数图象的平移,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c);平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能得出正确答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案