题目内容
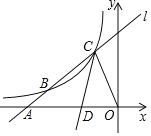
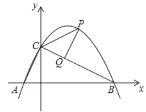
【题目】如图,二次函数![]() 的图象与y轴交于C点,交x轴于点A(-2,0),B(6,0),P是该函数在第一象限内图象上的动点,过点P作PQ⊥BC于点Q,连接PC,AC.
的图象与y轴交于C点,交x轴于点A(-2,0),B(6,0),P是该函数在第一象限内图象上的动点,过点P作PQ⊥BC于点Q,连接PC,AC.
(1)求该二次函数的表达式;
(2)求线段PQ的最大值;
(3)是否存在点P,使得以点P,C,Q为顶点的三角形与△ACO相似?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)PQ的最大值为
;(2)PQ的最大值为![]() ;(3)
;(3)![]() 或
或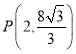
【解析】
(1)利用待定系数法,列出二元一次方程组求解即可得出结论;
(2)先确定出直线BC解析式,进而得出PM,再判断出△OAC∽△OCB,求出AC,进而得出∠MPQ的余弦值,即可得出结论;
(3)分两种情况,Ⅰ、当△QPC∽△OAC时,利用抛物线的对称性即可得出结论,Ⅱ、先确定出直线CD的解析式,联立抛物线解析式即可得出结论.
解:(1)将点A、B坐标代入抛物线解析式中得,
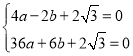 ,
,
∴解: ,
,
∴抛物线解析式为![]() ;
;
(2)设 ,
,![]()
令x=0,则![]() ,
,
∴![]() ,
,
∵B(6,0),
∴直线BC的解析式为![]() ,
,
如图1,过点P作PN⊥x轴于N,交BC于M,
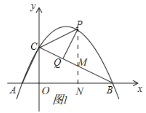
∴点 ,
,
∴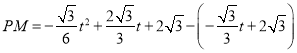
![]() ,
,
∵∠AOC=∠COB=∠CQP=∠POM=∠MDB=90°,
∵![]() ,
,
∴△OAC∽△OCB,
∴∠ACO=∠CBO=∠MPQ,
∴△OAC∽△OCB∽△NMB∽△QMP,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴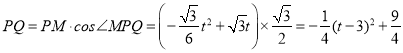
∴t=3时,PQ的最大值为![]() ;
;
(3)、①当△QPC∽△OAC时,
∴∠ACO=∠CBA=∠PCQ,
∴PC∥x轴,
由抛物线的对称性知,点C与点P关于P关于抛物线的对称轴对称,
∴![]() ;
;
②、当△QCP∽△OAC时,
∴∠CAO=∠PCQ,
∴tan∠CAO=tan∠PCQ,
如图2,过点B作BD⊥BC交CP的延长线于D,过点D作DE⊥x轴于E,
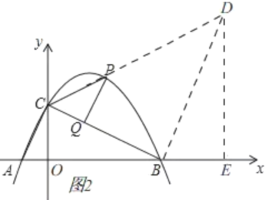
∴△OBC∽△EDB,
∴![]() ,
,
∴![]() ,
,
∴OE=OB+BE=12,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴直线CD的解析式为![]() ①
①
∵![]() ②,
②,
联立①②解得,
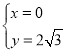 (舍)或
(舍)或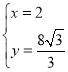 ,
,
∴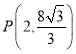 .
.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
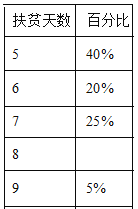
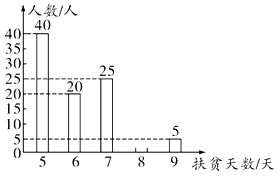
新思维寒假作业系列答案【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.