题目内容
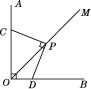
【题目】如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P放在射线OM上,两直角边分别与OA,OB交于点C,D.
(1)证明:PC=PD.
(2)若OP=4,求OC+OD的长度.
【答案】(1)见解析;(2)![]()
【解析】
(1)过点P点作PE⊥OA于E,PF⊥OB于F,根据垂直的定义得到∠PEC=∠PFD=90°,由OM是∠AOB的平分线,根据角平分线的性质得到PE=PF,利用四边形内角和定理可得到∠PCE+∠PDO=360°﹣90°﹣90°=180°,而∠PDO+∠PDF=180°,则∠PCE=∠PDF,然后根据“AAS”可判断△PCE≌△PDF,根据全等的性质即可得到PC=PD.
(2)由∠AOB=90°,OM平分∠AOB,得到△POE与△POF为等腰直角三角形,根据等腰三角形的性质有OE=PE=PF=OF,即可得到OE的长.由(1)知△PCE≌△PDF,由全等三角形对应边相等得到CE=DF,进而得到OC+OD=OE+OF=2OE,即可得出结论.
(1)如图,过点P作PE⊥OA于点E,PF⊥OB于点F,∴∠PEC=∠PFD=90°.
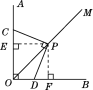
∵OM是∠AOB的平分线,∴PE=PF.
∵∠AOB=90°,∠CPD=90°,
∴∠PCE+∠PDO=360°-90°-90°=180°.
而∠PDO+∠PDF=180°,
∴∠PCE=∠PDF.
在△PCE和△PDF中,∵∠PCE=∠PDF,∠PEC=∠PFD,PE=PF,
∴△PCE≌△PDF(AAS)
∴PC=PD.
(2)∵∠AOB=90°,OM平分∠AOB,
∴△POE与△POF为等腰直角三角形,
∴OE=PE=PF=OF.
∵OP=4,
∴OE=![]() .
.
由(1)知△PCE≌△PDF,∴CE=DF,
∴OC+OD=OE+OF=2OE=![]() .
.