��Ŀ����
����Ŀ��ij������˾�ס����������̶�ͨ�������б���ij���칤����Ŀ����֪�ӵ����������̵�ʱ�����Ҷӵ�����������ʱ���![]() ���������Ҷӻ��������������ɼӵ�����55������ɼס������Ӻ���20�죬����˸�����칤������
���������Ҷӻ��������������ɼӵ�����55������ɼס������Ӻ���20�죬����˸�����칤������
���������������ס������ӵ�����ɸ��칤�������������죻
����������칤�̹�Ͷ��200��Ԫ���������ɵĹ����������ô�ס������ӿɻ̿��������Ԫ��
���𰸡���1���ӵ�����ɸ��칤��������100�죬�Ҷӵ�����ɸ��칤��������80�죻��2���ӿɻ̿�150���Ҷӿɻ̿�50��
��������
(1)�ѹ�������������λ1����ô�м������Ĺ�����+���Һ����Ĺ�����=1�������Ҷӵ��������Ҫx�죬����������Ҫ1.25x�죬���ݵ�����ϵʽ�з�ʽ���̲���⼴��.
(2)�ȼ����Ҷ���ɵĹ�������������ռ�������ɵó��Ҷӿɻ�õĹ��̿�̶��ó���õĹ��̿�.
�⣺������ס������ӵ�����ɸ��칤���������1.25x�죬x��
������ã�![]()
�����ã�![]()
��ã� x��80��
�����飺x��80��ԭ���̵Ľ⣮
��1.25x=100(��)
�𣺼ӵ�����ɸ��칤��������100�죬�Ҷӵ�����ɸ��칤��������80�죻
�����Ҷ���ɵĹ�����![]()
�Ҷӿɻ̿![]() ��50����
��50����
�ӿɻ̿200-50=150����
�𣺼ӿɻ̿�150���Ҷӿɻ̿�50��

����Ŀ��������ijѧУ�������飬A��ѧ���ﹲ��������B��ѧ������������˽�ҳ��ȣ�C��ѧ�����У�D��ѧ���������������ݵ����������˲�������ͳ��ͼ��
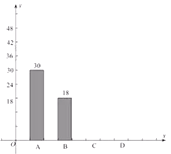
���� | Ƶ�� | Ƶ�� |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
��1��ѧ����________�ˣ� ![]() ________��
________�� ![]() ________��
________��
��2����ȫ����ͳ��ͼ��
��3������У����2000�ˣ��ﹲ����������________�ˣ�