题目内容
【题目】如图所示，在平面直角坐标系中，O为坐标原点，直线y＝kx+b经过点A（﹣2，﹣1），交y轴负半轴于点B，且∠ABO＝30°，过点A作直线AC⊥x轴于点C，点P在直线AC上．
（1）k＝ ；b＝ ；
（2）设△ABP的面积为S，点P的纵坐标为m．
①当m＞0时，求S与m之间的函数关系式；
②当S＝2时，求m的值；
③当m＞0且S＝4时，以BP为边作等边△BPQ，请直接写出符合条件的所有点Q的坐标．
【答案】（1）k＝﹣
；b＝﹣1﹣2；（2）①S＝1+m；②m的值为1或﹣3；③点Q的坐标为（﹣4﹣2，1﹣2）或（2+2，1）
【解析】
（1）CD=
AC=，AD=2CD=
，则B（0，-1-2），把点B和A（-2，-1）代入y=kx+b，即可求解；
（2）①当m＞0，△ABP的面积为S=
（1+m）×2=1+m，即S=1+m；
②-1＜m≤0时，△ABP的面积为S=（1+m）×2=1+m，即S=1+m；当m＜-1时，△ABP的面积为S=（-1-m）×2=-1-m，即S=-1-m；即可求解；
③以证明△BPQ是等边三角形、△BQE≌△PBF（AAS），、△PQ'G≌△PBF（AAS），即可求解．
解：（1）设直线y＝kx+b与x轴交于点D，如图所示：
∵点A（﹣2，﹣1），
∴OC＝2，AC＝1，
∵AC⊥x轴，OB⊥x轴，
∴AC∥OB，
∴∠CAD＝∠ABO＝30°，
∴CD＝AC＝，
∴AD＝2CD＝，
OD＝CD+OC＝+2，
∴BD＝2OD＝+4，OB＝
OD＝1+2，
∴B（0，﹣1﹣2），
把点B和A（﹣2，﹣1）代入y＝kx+b得：并解得：
∴y＝﹣x﹣1﹣2，
故答案为：﹣；
（2）①当m＞0，如图1所示：
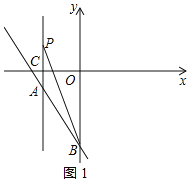
则PC＝m，AP＝AC+PC＝1+m，
∴△ABP的面积为S＝（1+m）×2＝1+m，即S＝1+m；
②﹣1＜m≤0时，如图2所示：
则AP＝1+m，
∴△ABP的面积为S＝（1+m）×2＝1+m，即S＝1+m；
当m＜﹣1时，如图3所示：
则AP＝﹣1﹣m，
∴△ABP的面积为S＝（﹣1﹣m）×2＝﹣1﹣m，即S＝﹣1﹣m；
把S＝2代入S＝1+m得：2＝1+m，
解得：m＝1；
把S＝2代入S＝﹣1﹣m得：2＝﹣1﹣m，
解得：m＝﹣3；
综上所述，当S＝2时，m的值为1或﹣3；
③以BP为边作等边△BPQ和等边△BPQ'，作QE⊥y轴于E，PF⊥y轴于F，如图4所示：
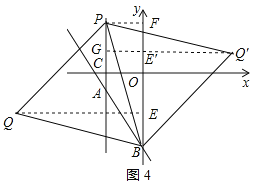
则PF＝2，OF＝3，BF＝OF+OB＝4+2，
当m＞0且S＝4时，4＝1+m，
解得：m＝3，
∴P（﹣2，3），
∴PC＝3，AP＝1+3＝4，
∵AB＝BD﹣AD＝4，
∴AP＝AB，
∴∠ABP＝∠APB＝∠CAD＝15°，
∵AC∥OB，
∴∠PBF＝∠APB＝15°，
∵△BPQ是等边三角形，
∴BQ＝BP，∠PBQ＝60°，
∴∠QBE＝75°，∴∠BQE＝90°﹣75°＝15°＝∠PBF，
在△BQE和△PBF中，
∠QEB＝∠BFP＝90°，∠BQE＝∠PBF，BQ＝PB，
∴△BQE≌△PBF（AAS），
∴QE＝BF＝4+2，BE＝PF＝2，
∴OE＝OB﹣BE＝2﹣1，
∴点Q的坐标为（﹣4﹣2，1﹣2）；
作Q'G⊥PC于G，交y轴于E'，
同理：△PQ'G≌△PBF（AAS），
∴Q'G＝BF＝4+2，PG＝PF＝2，
∴OE'＝Q'G﹣OC＝2+2，CG＝PC﹣PG＝1，
∴点Q'的坐标为（2+2，1）；
综上所述，点Q的坐标为（﹣4﹣2，1﹣2）或（2+2，1）．
