题目内容
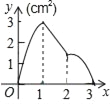
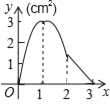
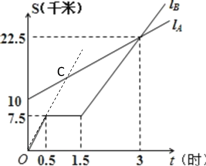
【题目】如图，lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米；
(2)走了一段路后，自行车发生故障，进行修理，所用的时间是______小时；
(3)B再次出发后______小时与A相遇；
(4)求出A行走的路程S与时间t的函数关系式(写出过程)；
(5)若B的自行车不发生故障，保持出发时的速度前进，几小时与A相遇？在图中表示出这个相遇点C.
【答案】（1）10；（2）1；（3）1.5；（4）
；（5）
小时，画图见解析.
【解析】
（1）根据图像和题意，当t=0即可得出结论；
（2）观察图像即可得出结论；
（3）观察图像即可得出结论；
（4）设直线lA的解析式为S=kt+b（k≠0），然后分别将（0,10）和（3，22.5）代入即可求出A行走的路程S与时间t的函数关系式；
（5）根据题意，分别求出A、B的速度，然后根据公式：追及时间=路程差÷速度差，即可求出B追上A所需的时间，最后画图即可.
解：（1）由图像可知：当t=0时，B与A相距10千米
故答案为10；
（2）由图像可知：修理自行车所用的时间为：1.5－0.5=1小时
故答案为：1；
（3）由图像可知：B再次出发后，3－1.5=1.5小时与A相遇
故答案为：1.5；
（4）设直线lA的解析式为S=kt+b（k≠0），
分别将（0,10）和（3，22.5）代入，得
解得：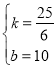
∴A行走的路程S与时间t的函数关系式为：；
（5）由图像可知：A的速度为：（22.5－10）÷3=
（千米/小时）
若B的自行车不发生故障，B的速度为：7.5÷0.5=15（千米/小时）
A、B的路程差为：10千米
∴若B的自行车不发生故障，B追上A所需的时间为：10÷（15－）=小时.
如下图所示，点C即为所求.
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
