题目内容
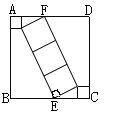
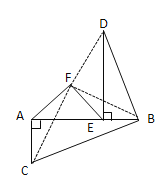
【题目】已知:AB⊥AC,DE⊥AB,AC=BE,BC=BD,

(1)求证:BC⊥BD;
(2)若点F是BC,BD的垂直平分线的交点,连接FA、FE.填空:判断△AFE的形状是_____.
【答案】(1)证明见解析;(2)等腰直角三角形
【解析】
(1)利用HL定理证明Rt△ABC≌Rt△EDB,然后得到∠D=∠ABC,从而求证;(2)连接FC,FB,FD,利用垂直平分线的性质
证明:(1)∵AB⊥AC,DE⊥AB
∴∠CAB=∠BED=90°
在Rt△ABC≌Rt△EDB中,![]()
∴Rt△ABC≌Rt△EDB(HL)
∴∠D=∠ABC
又∵∠DBE+∠ABC=90°
∴∠D+∠ABC=90°
∴∠CBD=90°
即BC⊥BD;
(2)连接FC,FB,FD,
∵点F是BC,BD的垂直平分线的交点
∴FC=FB=FD
∴∠CBF=∠FCB
又∵BC=BD,BF=BF
∴△BCF≌△BDF
又∵∠CBD=90°
∴∠DBF=∠CBF=45°
∴∠FCB=∠DBF=∠CBF=45°
∴∠CFB=90°
又∵Rt△ABC≌Rt△EDB
∴∠ACB=∠DBE,AC=BE
∴∠ACF=∠EBF
又∵FC=FB
∴△FAC≌△FEB
∴FA=FE,∠AFC=∠EFB
∵∠CFB=90°
∴∠CFE+∠EFB=90°
∴∠AFC+∠EFB=90°
即∠AFE=90°
即△AFE是等腰直角三角形

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目