题目内容
(2011•攀枝花)如图,在等腰梯形ABCD中,AD∥BC,AB=CD=AD,∠B=60°,DE⊥AC于点E,已知该梯形的高为 .
.
(1)求证:∠ACD=30°;
(2)DE的长度.
 .
.(1)求证:∠ACD=30°;
(2)DE的长度.

解:(1)∵AD∥BC,
∴∠DAC=∠BCA,
∵AB=CD=AD,
∴∠DAC=∠DCA,∠DCB=∠B=60°,
∴∠DCA=∠BCA,
∴∠ACD=30°;
(2)作DG⊥BC于G点,
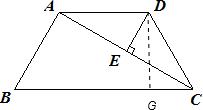
∵∠B=60°,梯形的高 为
为 ,
,
∴DC=DG÷sin∠DCG= ÷
÷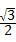 =2,
=2,
∴DE=DC×sin∠ACD=2×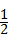 =1.
=1.
∴DE的长为1.
∴∠DAC=∠BCA,
∵AB=CD=AD,
∴∠DAC=∠DCA,∠DCB=∠B=60°,
∴∠DCA=∠BCA,
∴∠ACD=30°;
(2)作DG⊥BC于G点,

∵∠B=60°,梯形的高
 为
为 ,
,∴DC=DG÷sin∠DCG=
 ÷
÷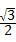 =2,
=2,∴DE=DC×sin∠ACD=2×
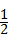 =1.
=1.∴DE的长为1.
略

练习册系列答案
相关题目




 -sin
-sin 45
45


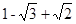
 的正上方
的正上方 处测得月亮山山顶
处测得月亮山山顶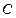 的
的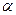 ,在月亮山山顶
,在月亮山山顶 处测得东方山山顶
处测得东方山山顶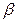 ,如图(7)。已知
,如图(7)。已知 ,若飞机的飞行速度为180米/秒,则该飞机从
,若飞机的飞行速度为180米/秒,则该飞机从

 ,
, ,
,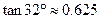 )
)