题目内容
【题目】(1)(问题发现)如图1,△ABC和△ADE均为等边三角形,点B,D,E在同一条直线上.填空:①线段BD,CE之间的数量关系为 ;②∠BEC = °.
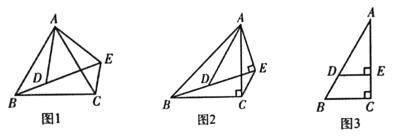
(2)(类比探究)如图2,△ABC和△ADE均为等腰直角三角形,∠ACB=∠AED=90°,AC=BC,AE=DE,点B,D,E在同一条直线上,请判断线段BD,CE之间的数量关系及∠BEC的度数,并给出证明.
(3)如图3,在△ABC中,∠ACB=90°,∠A=30°,AB = 5,点D在AB 边上,DE⊥AC于点E,AE = 3,将△ADE绕点A旋转,当DE所在直线经过点B时,CE的长是多少?(直接写出答案)
【答案】(1)①BD=CE,②60;(2)BD=![]() ,∠BEC=45
,∠BEC=45![]() .理由见解析;(3)
.理由见解析;(3)![]() 或
或![]()
【解析】
(1)利用等边三角形的性质和SAS可证明![]() ,则有
,则有![]() ,然后再利用
,然后再利用![]() 即可求出
即可求出![]() 的度数;
的度数;
(2)首先利用等腰直角三角形的性质和锐角三角函数得出![]() ,则有
,则有![]() ,
,![]() ,进而可求出
,进而可求出![]() ,再根据
,再根据![]() 即可得到
即可得到![]() ;
;
(3)分两种情况进行讨论:将△ADE绕点A顺时针旋转,DE所在直线经过点B时和将△ADE绕点A逆时针旋转,DE所在直线经过点B时,利用相似三角形的判定及性质求解即可.
解:(1)∵![]() 和
和![]() 均为等边三角形,
均为等边三角形,
![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,
![]() ;
;
(2)![]() ,
,![]() .
.
理由如下:![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() 和
和![]() 中,
中,
![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]()
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
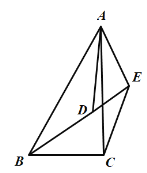
(3)如图,将△ADE绕点A逆时针旋转,DE所在直线经过点B时,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
如图,将△ADE绕点A顺时针旋转,DE所在直线经过点B时,

同理可得![]() ,
,
综上所述,CE的长度为![]() 或
或![]() .
.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目