题目内容
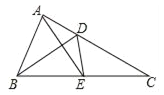
【题目】如图，将△ABC沿角平分线BD所在直线翻折，顶点A恰好落在边BC的中点E处，AE=BD，那么tan∠ABD=（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
作CM⊥AE交AE的延长线于M，作DN⊥AB于N，DF⊥BC于F，AE与BD交于点K，设DK=a，先证明AD：CD=1：2，再证明△BKE≌△CME，得BK=CM=3a，根据tan∠ABD=
即可解决问题．
如图，作CM⊥AE交AE的延长线于M，作DN⊥AB于N，DF⊥BC于F，AE与BD交于点K，设DK=a．
∵AB=BE=EC，∴BC=2AB．
∵DB平分∠ABC，∴DN=DF．
∵
，∴
．
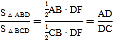∵AB=FB，∠ABD=∠EBD，∴DB⊥AM，AK=KE．
∵DB⊥AM，CM⊥AM，∴DK∥CM，∴
，∠KBE=∠MCE，∴CM=3a．在△BKE和△CME中，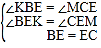
，∴△BKE≌△CME，∴BK=CM=3a，∴BD=AE=4a，∴AK=KE=2a，∴tan∠ABD=
．
故选B．
练习册系列答案
春雨教育同步作文系列答案
相关题目
【题目】一般成年人的脚长（厘米）与鞋码（码）有如下关系：
脚长 | 23 | 23．5 | 24 | 24．5 | … |
鞋码 | 36 | 37 | 38 | 39 | … |
（1）若某人的脚长为26厘米，他应穿多少码的鞋？
（2）请建立鞋码
（厘米）与脚长
（码）之间的函数表达式；
（3）我国著名篮球运动员姚明穿53码的鞋，请你根据以上关系计算他的脚长．
【题目】抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y，的对应值如下表：
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
（1）根据上表填空：
①抛物线与x轴的交点坐标是_________和_________；
②抛物线经过点（-3，_________）；
（2）试确定抛物线y=ax2+bx+c的解析式.
