题目内容
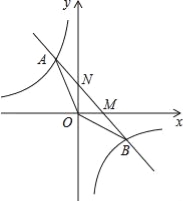
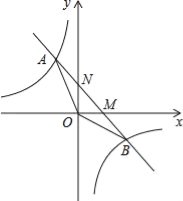
【题目】如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数![]() 的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
(1)求一次函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出y1>y2时x的取值范围.
【答案】(1)y1=﹣x+2,(2)6;(3)x<﹣2或0<x<4
【解析】
试题分析:(1)先根据反比例函数解析式求得两个交点坐标,再根据待定系数法求得一次函数解析式;
(2)将两条坐标轴作为△AOB的分割线,求得△AOB的面积;
(3)根据两个函数图象交点的坐标,写出一次函数图象在反比例函数图象上方时所有点的横坐标的集合即可.
试题解析:(1)设点A坐标为(﹣2,m),点B坐标为(n,﹣2)
∵一次函数y1=kx+b(k≠0)的图象与反比例函数y2=﹣![]() 的图象交于A、B两点
的图象交于A、B两点
∴将A(﹣2,m)B(n,﹣2)代入反比例函数y2=﹣![]() 可得,m=4,n=4
可得,m=4,n=4
∴将A(﹣2,4)、B(4,﹣2)代入一次函数y1=kx+b,可得
![]() ,解得
,解得![]()
∴一次函数的解析式为y1=﹣x+2;,
(2)在一次函数y1=﹣x+2中,
当x=0时,y=2,即N(0,2);当y=0时,x=2,即M(2,0)
∴![]() =
=![]() ×2×2+
×2×2+![]() ×2×2+
×2×2+![]() ×2×2=2+2+2=6;
×2×2=2+2+2=6;
(3)根据图象可得,当y1>y2时,x的取值范围为:x<﹣2或0<x<4

 名校课堂系列答案
名校课堂系列答案【题目】盈盈超市第一次用6000元购进甲,乙两种商品,其中乙商品的件数比甲商品件数的 ![]() 多15件,甲,乙两种商品的进价和零售价如下表(注:获利=售价﹣进价):
多15件,甲,乙两种商品的进价和零售价如下表(注:获利=售价﹣进价):
甲 | 乙 | |
进价(件/元) | 22 | 30 |
售价(件/元) | 29 | 40 |
(1)第一次进货时甲,乙两种商品各购进多少件?
(2)该超市第二次以第一次的进价又购进甲,乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍,甲商品按原价销售,乙商品打折销售.第二次两种商品都销售完后盈利2130元,求第二次乙种商品是按原价打几折销售的.