题目内容
【题目】阅读下面材料，完成（1）﹣（3）题
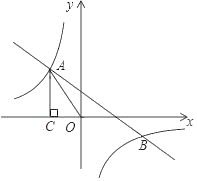
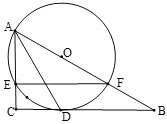
数学课上，老师出示了这样一道题：如图1，
中，
，点
在
上，
，
（其中
）
，
的平分线与相交于点
，
垂足为
，探究线段
与
的数量关系，并证明．同学们经过思考后，交流了自已的想法：
小明：“通过观察和度量，发现
与
相等．”
小伟：“通过构造全等三角形，经过进一步推理，可以得到线段与的数量关系．”
……
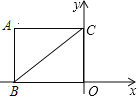
老师：“保留原题条件，延长图1中的，与相交于点
（如图2），可以求出
的值．”
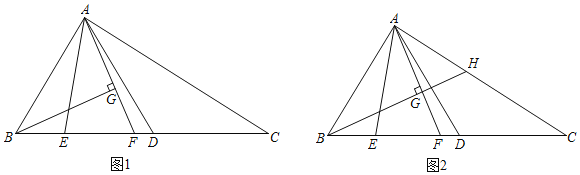
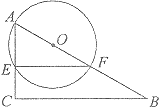
（1）求证：
；
（2）探究线段与的数量关系（用含
的代数式表示），并证明；
（3）直接写出的值（用含的代数式表示）．
【答案】（1）见解析；（2）
；（3）
【解析】
（1）利用三角形的外角性质可求解；
（2）由直角三角形的性质和角平分线的性质可得AF=FC，AF=BF，通过证明△ABG∽△BCA和△ABF∽△BAD，利用相似三角形的性质可求解；
（3）通过证明△ABH∽△ACB，可得AB2=AC×AH，设BD=m，AB=km，由勾股定理可求AC的长，可求AH，HC的长，即可求解．
证明：（1）∵
∴
∵
,
∴
（2）设
，
∴
∵
，
∴
∵
平分
∴
∴
，
∴
∴
∵
，
∴
∽
∴
∵，
∴
∽
∴
，且
，
∴
，即
∴
（3）∵，
∴
，且
∴
∽
∴
∴
设
，
∵
∴
∴
∴
∴
∴
∴
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
