题目内容
【题目】在平行四边形ABCD中，∠A＝30°，AD＝
，BD＝4，则平行四边形ABCD的面积等于 ______________.
【答案】
或
【解析】
过点D作DE⊥AB，垂足为E，分点E在AB上或AB的延长线上两种情况，分别利用三角函数求出AE、DE的长，利用勾股定理求出BE的长，继而可得AB的长，然后利用平行四边形的面积公式进行求解即可.
过点D作DE⊥AB，垂足为E，
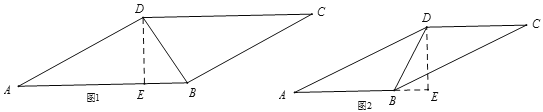
如图1，点E在AB上，
∵∠A=30°，∴DE=ADsin30°=
，AE=ADcos30°=6，
在Rt△DBE中，BE=
，
∴AB=AE+BE=8，
∴平行四边形ABCD的面积为
；
如图2，点E在AB的延长线上，
∵∠A=30°，∴DE=ADsin30°=，AE=ADcos30°=6，
在Rt△DBE中，BE=，
∴AB=AE-BE=4，
∴平行四边形ABCD的面积为
，
故答案为：或.
练习册系列答案
相关题目
