题目内容
【题目】如图,∠AOB=30°,点P是∠AOB内的定点,且OP=3.若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )

A.12B.9C.6D.3
【答案】D
【解析】
根据题意,作点P关于OA、OB的对称点E、D,连接DE,与OA相交于点M,与OB相交于点N,则此时△PMN周长的最小值是线段DE的长度,连接OD、OE,由∠AOB=30°,得到∠DOE=60°,由垂直平分线的性质,得到OD=OE=OP=3,则△ODE是等边三角形,即可得到DE的长度.
解:如图:作点P关于OA、OB的对称点E、D,连接DE,与OA相交于点M,与OB相交于点N,则此时△PMN周长的最小值是线段DE的长度,连接OD、OE,
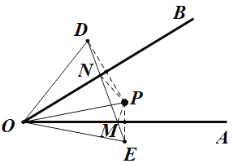
由垂直平分线的性质,得DN=PN,MP=ME,OD=OE=OP=3,
∴△PMN周长的最小值是:PN+PM+MN=DN+MN+ME=DE,
由垂直平分线的性质,得∠DON=∠PON,∠POM=∠EOM,
∴∠DOE=∠DOP+∠EOP=2(∠PON+∠POM)=2∠MON=60°,
∴△ODE是等边三角形,
∴DE=OD=OE=3,
∴△PMN周长的最小值是:PN+PM+MN=DE=3;
故选:D.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目