题目内容
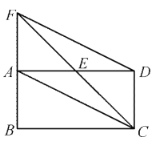
【题目】如图,矩形![]() 中,点
中,点![]() 是
是![]() 的中点,延长
的中点,延长![]() ,
,![]() 交于点
交于点![]() ,连结
,连结![]() ,
,![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 平分
平分![]() 时,写出
时,写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)见详解;(2)BC=2CD,理由见详解
【解析】
(1)根据矩形的性质可知AB∥CD,再根据三角形全等的判定和性质,证得AF=CD,根据平行四边形的判定求得结论即可;
(2)结论是:BC=2CD.由矩形性质可知∠BCD=90°,当![]() 平分
平分![]() 时,∠BCF=45°,得出BC和BF的关系,进而得出结论.
时,∠BCF=45°,得出BC和BF的关系,进而得出结论.
证明:(1)∵矩形![]()
∴AB∥CD
∴∠AFE=∠DCE,∠FAE=∠CDE
∵AE=DE
∴△AFE≌△DCE∴AF=DC
∴四边形![]() 是平行四边形;
是平行四边形;
(2)![]() 与
与![]() 的数量关系是:BC=2CD.
的数量关系是:BC=2CD.
理由是:∵矩形![]()
∴∠B=∠BCD=90°
∵![]() 平分
平分![]()
∴∠BCF=45°
∴∠BFC=45°
∴BC=BF=2AF=2CD
即BC=2CD

练习册系列答案
相关题目