题目内容
【题目】在学习了轴对称知识之后，数学兴趣小组的同学们对课本习题进行了深入研究，请你跟随兴趣小组的同学，一起完成下列问题．
(1)（课本习题）如图①，△ABC是等边三角形，BD是中线，延长BC至E，使CE=CD． 求证：DB=DE
(2)（尝试变式）如图②，△ABC是等边三角形，D是AC边上任意一点，延长BC至E，使CE=AD．
求证：DB=DE．
(3)（拓展延伸）如图③，△ABC是等边三角形，D是AC延长线上任意一点，延长BC至E，使CE=AD请问DB与DE是否相等? 并证明你的结论．
【答案】（1）见详解；（2）见详解；（3）DB=DE成立，证明见详解
【解析】
（1）由等边三角形的性质，得到∠CBD=30°，∠ACB=60°，由CD=CE，则∠E=∠CDE=30°，得到∠E=∠CBD=30°，即可得到DB=DE；
（2）过点D作DG∥AB，交BC于点G，证明△BDC≌△EDG，根据全等三角形的性质证明结论；
（3）过点D作DF∥AB交BE于F，由“SAS”可证△BCD≌△EFD，可得DB=DE．
证明：（1）∵△ABC是等边三角形
∴∠ABC=∠BCA=60°，
∵点D为线段AC的中点，
∴BD平分∠ABC，AD=CD，
∴∠CBD=30°，
∵CD=CE，
∴∠CDE=∠CED，
又∵∠CDE+∠CED=∠BCD，
∴2∠CED=60°，
∴∠CED=30°=∠CBD，
∴DB=DE；
（2）过点D作DG∥AB，交BC于点G，如图，
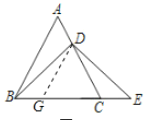
∴∠DGC=∠ABC=60°，又∠DCG=60°，
∴△DGC为等边三角形，
∴DG=GC=CD，
∴BC-GC=AC-CD，即AD=BG，
∵AD=CE，
∴BG=CE，
∴BC=GE，
在△BDC和△EDG中，
，
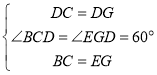∴△BDC≌△EDG（SAS）
∴BD=DE；
（3）DB=DE成立，
理由如下：过点D作DF∥AB交BE于F，
∴∠CDF=∠A，∠CFD=∠ABC，
∵△ABC是等边三角形
∴∠ABC=∠BCA=∠A=60°，BC=AC=AB，
∴∠CDF=∠CFD=60°=∠ACB=∠DCF，
∴△CDF为等边三角形
∴CD=DF=CF，
又AD=CE，
∴AD-CD=CE-CF，
∴BC=AC=EF，
∵∠BCD=∠CFD+∠CDF=120°，
∠DFE=∠FCD+∠FDC=120°，
∴∠BCD=∠DFE，且BC=EF，CD=DF，
∴△BCD≌△EFD（SAS）
∴DB=DE．
