题目内容
【题目】如图,在平面直角坐标系xOy中,A点的坐标为(1,0).以OA为边在x轴上方画一个正方形OABC.以原点O为圆心,正方形的对角线OB长为半径画弧,与x轴正半轴交于点D.

(1)点D的坐标是 ;
(2)点P(x,y),其中x,y满足2x-y=-4.
①若点P在第三象限,且△OPD的面积为3![]() ,求点P的坐标;
,求点P的坐标;
②若点P在第二象限,判断点E(![]() +1,0)是否在线段OD上,并说明理由.
+1,0)是否在线段OD上,并说明理由.
【答案】(1)(![]() ,0);(2)①P(-5,-6);②点E在线段OD上,见解析.
,0);(2)①P(-5,-6);②点E在线段OD上,见解析.
【解析】
(1)先求出正方形的边长,再用勾股定理求出OB,即可得出结论;
(2)①先表示出PQ,再利用△ODP的没解决建立方程求解,即可得出结论;
②根据点P在第二象限,求出x的范围,进而判断出点E在x轴正半轴上,即可得出结论.
(1)∵四边形OABC是正方形,且A(1,0),
∴OA=AB=1,
根据勾股定理得,OB=![]() ,
,
∴OD=![]() ,
,
∴D(![]() ,0),
,0),
故答案为:(![]() ,0);
,0);
(2)①如图,过点P作PQ⊥x轴于点Q,
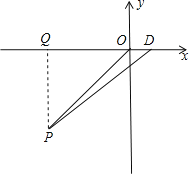
∵点P在第三象限,
∴y=2x+4<0,
∴PQ=-(2x+4),
∵D(![]() ,0),
,0),
∴OD=![]() ,
,
∴S△ODP=![]() ODPQ=3
ODPQ=3![]() ,
,
即:-![]() ×
×![]() ×(2x+4)=3
×(2x+4)=3![]() ,
,
∴x=-5,
∴P(-5,-6);
②点E在线段OD上,
理由:∵2x-y=-4,
∴y=2x+4,
∵点P在第二象限,
∴![]() ,
,
∴-2<x<0,
∴0<![]() x+1<1,
x+1<1,
∴点E在x轴正半轴上,
∵点D在x轴正半轴,OD=![]() ,
,
∴0<OE<OD,
∴点E在线段OD上.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目










