题目内容
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
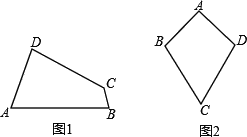
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=78°,∠B=82°,则∠C=_________,∠D=__________
(2)在探究“等对角四边形”性质时:
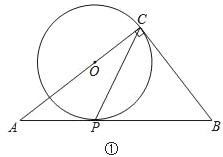
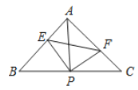
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例(提示:举反例可画图并说明)
(3)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=![]() ,AD=
,AD=![]() ,求对角线AC的长.
,求对角线AC的长.
【答案】(1)118°,82°;(2)①见解析,②小红的猜想不正确,反例见解析;(3)AC的长为![]() 或
或![]()
【解析】
(1)根据四边形ABCD是“等对角四边形”得出∠D=∠B=82°,根据多边形内角和定理求出∠C即可;
(2)①连接BD,根据等边对等角得出∠ABD=∠ADB,求出∠CBD=∠CDB,根据等腰三角形的判定得出即可;
②不正确.举一个使其结论不成立的反例即可.
(3)分两种情况讨论:当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,利用勾股定理求解;当∠BCD=∠DAB=60°时,过点D作DE⊥AB于点E,DF⊥BC于点F,求出线段利用勾股定理求解.
(1)∵四边形ABCD是“等对角四边形”,∠A≠∠C,∠B=82°,
∴∠D=∠B=82°
∴∠C=360°-∠A-∠B-∠D=118°
故答案为:118°,82°
(2)①如图,连接BD,

∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC,
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB,
∴∠CBD=∠CDB,
∴CB=CD;
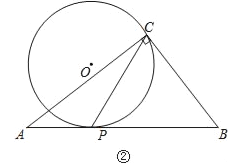
②小红的猜想不正确,如图:
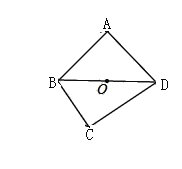
四边形ABCD是“等对角四边形”∠A=∠C=90°,AB=AD,但![]() ,
,
所以小红的猜想不正确;
(3)分两种情况:
①当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,如图:
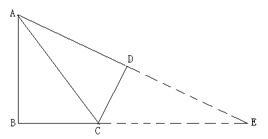
∵∠ABC=90°,∠DAB=60°,AB=![]() ,
,
∴∠E=30°,
∴AE=2AB=![]() ,
,
∴DE=AE﹣AD=![]() ,
,
∵∠EDC=90°,∠E=30°,
∴CD=![]() 6,
6,
∴AC=![]() =
=![]() ;
;
②当∠BCD=∠DAB=60°时,
过点D作DM⊥AB于点M,DN⊥BC于点N,如图:
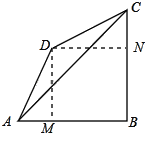
则∠AMD=90°,四边形BNDM是矩形,
∵∠DAB=60°,
∴∠ADM=30°,
∴AM=![]() AD=
AD=![]() ,
,
∴DM=![]() 6
6
∴BM=AB﹣AM=![]() ,
,
∵四边形BNDM是矩形,
∴DN=BM=![]() ,BN=DM=6,
,BN=DM=6,
∵∠BCD=60°,
∴CN=![]() 3,
3,
∴BC=CN+BN=9,
∴AC=![]()
![]() ;
;
综上所述:AC的长为![]() 或
或![]()
![]()

 步步高达标卷系列答案
步步高达标卷系列答案【题目】某城市为创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶(如图所示),据调查该城市的A、B、C三个社区积极响应号并购买,具体购买的数和总价如表所示.
社区 | 甲型垃圾桶 | 乙型垃圾桶 | 总价 |
A | 10 | 8 | 3320 |
B | 5 | 9 | 2860 |
C | a | b | 2820 |
(1)运用本学期所学知识,列二元一次方程组求甲型垃圾桶、乙型垃圾桶的单价每套分别是多少元?
(2)按要求各个社区两种类型的垃圾桶都要有,则a= .