Question

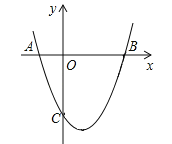
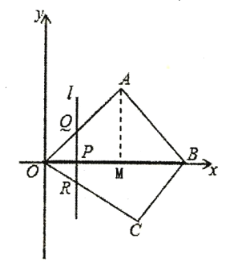
【题目】如图，在平面直角坐标系中，四边形的顶点是坐标原点，点在第一象限，点在第四象限，点在轴的正半轴上．且，，的长分别是二元一次方程组的解（）．

（1）求点和点的坐标；

（2）点是线段上的一个动点（点不与点，重合），过点的直线与轴平行，直线交边或边于点，交边或边于点．设点的横坐标为，线段的长度为．已知时，直线恰好过点．

①当时，求关于的函数关系式；

②当时，求点的横坐标的值．

Answer 1

【答案】（1）A（3，3），B（6，0）；（2）当时，；（3）满足条件的P的坐标为（2，0）或

【解析】

（1）解方程组得到OB，OC的长度，得到B点坐标，再根据△OAB是等腰直角三角形，解出点A的坐标；

（2）①根据坐标系中两点之间的距离，QR的长度为点Q与点R纵坐标之差，根据OC的函数解析式，表达出点R坐标，根据△OPQ是等腰直角三角形得出点Q坐标，表达m即可；

②根据直线l的运动时间分类讨论，分别求出直线AB，直线BC的解析式，再由QR的长度为点Q与点R纵坐标之差表达出m的函数解析式，当时，列出方程求解．

解：（1）如图所示，过点A作AM⊥OB，交OB于点M，

解二元一次方程组，得：，

∵，

∴OB=6，OC=5

∴点B的坐标为（6，0）

∵∠OAB=90°，OA=AB，

∴△OAB是等腰直角三角形，∠AOM=45°，

根据等腰三角形三线合一的性质可得，

∵∠AOM=45°，则∠OAM=90°-45°=45°=∠AOM，

∴AM=OM=3，所以点A的坐标为（3，3）

∴A（3，3），B（6，0）

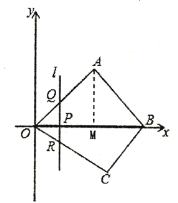
（2）①由（1）可知，∠AOM=45°，

又PQ⊥OP，

∴△OPQ是等腰直角三角形，

∴PQ=OP=t,

∴点Q（t，t）

如下图，过点C作CD⊥OB于点D，

∵时，直线恰好过点，

∴OD=4，OC=5

在Rt△OCD中，CD=

∴点C（4，-3）

设直线OC解析式为y=kx，

将点C代入得-3=4k，

∴，

∴，

∴点R（t，）

∴

故当时，

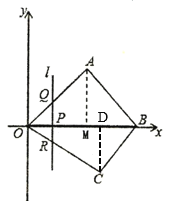
②设AB解析式为

将A（3，3）与点B（6，0）代入得

，解得

所以直线AB的解析式为，

同理可得直线BC的解析式为

当时，若，则，解得t=2，∴P（2，0）

当时，，若，即，解得t=10（不符合，舍去）

当时，Q（t，-t+6），R（t，）

∴

若，即，解得，此时，

综上所述，满足条件的P的坐标为（2，0）或．