题目内容
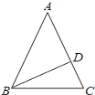
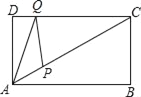
【题目】![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() 和
和![]() 上的动点,在图中画出
上的动点,在图中画出![]() 值最小时的图形,并直接写出
值最小时的图形,并直接写出![]() 的最小值为 .
的最小值为 .
【答案】作图见解析,![]()
【解析】
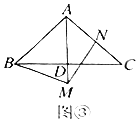
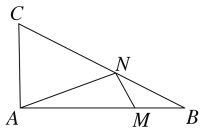
作A点关于BC的对称点A',A'A与BC交于点H,再作A'M⊥AB于点M,与BC交于点N,此时AN+MN最小,连接AN,首先用等积法求出AH的长,易证△ACH≌△A'NH,可得A'N=AC=4,然后设NM=x,利用勾股定理建立方程求出NM的长,A'M的长即为AN+MN的最小值.
如图,作A点关于BC的对称点A',A'A与BC交于点H,再作A'M⊥AB于点M,与BC交于点N,此时AN+MN最小,最小值为A'M的长.

连接AN,
在Rt△ABC中,AC=4,AB=8,
∴BC=![]()
∵![]()
∴AH=![]()
∵CA⊥AB,A'M⊥AB,
∴CA∥A'M
∴∠C=∠A'NH,
由对称的性质可得AH=A'H,∠AHC=∠A'HN=90°,AN=A'N
在△ACH和△A'NH中,
∵∠C=∠A'NH,∠AHC=∠A'HN,AH=A'H,
∴△ACH≌△A'NH(AAS)
∴A'N=AC=4=AN,
设NM=x,
在Rt△AMN中,AM2=AN2-NM2=![]()
在Rt△AA'M中,AA'=2AH=![]() ,A'M=A'N+NM=4+x
,A'M=A'N+NM=4+x
∴AM2=AA'2-A'M2=![]()
∴![]()
解得![]()
此时![]() 的最小值=A'M=A'N+NM=4+
的最小值=A'M=A'N+NM=4+![]() =
=![]()

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目