题目内容
【题目】二次函数y=ax2﹣2ax﹣3(a≠0)的图象经过点A.
(1)求二次函数的对称轴;
(2)当A(﹣1,0)时,
①求此时二次函数的表达式;
②把y=ax2﹣2ax﹣3化为y=a(x﹣h)2+k的形式,并写出顶点坐标;
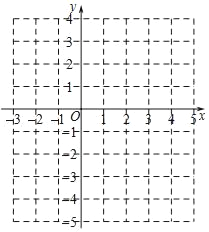
③画出函数的图象.
【答案】(1)x=1;(2)①y=x2﹣2x﹣3;②y=(x﹣1)2﹣4,顶点坐标为(1,﹣4);③见解析.
【解析】
(1)对于一般形式的二次函数y=ax2+bx+c,对称轴为x=![]() .
.
(2)①图象过(﹣1,0)点,将该点代入函数关系式即可求出参数.
②通过配方,得到二次函数的顶点式,从而写出顶点坐标.
(3)与x轴的交点即令y=0求出的x的值就是交点的横坐标,本题可以根据因式分解的方法求一元二次方程的根.
解:(1)二次函数y=ax2﹣2ax﹣3的对称轴是直线x=﹣![]() ,即x=1;
,即x=1;
(2)①∵二次函数y=ax2﹣2ax﹣3(a≠0)的图象经过点A(﹣1,0),
∴a+2a﹣3=0,
∴a=1,
∴此时二次函数的表达式为y=x2﹣2x﹣3;
②y=x2﹣2x﹣3=(x﹣1)2﹣4,
顶点坐标为(1,﹣4);
③∵y=x2﹣2x﹣3,
∴y=0时,x2﹣2x﹣3=0,解得x=﹣1或3,
∴函数与x轴的交点为(﹣1,0),(3,0).
函数的图象如图所示:

练习册系列答案
相关题目