题目内容
已知a+b=3，a3+b3=9，则ab等于
- A.1
- B.2
- C.3
- D.4
B
分析：根据条件a+b=3，两边平方可求得a2+b2=9-2ab，再把条件a3+b3=9展成（a+b）和ab的形式，整体代入即可求得ab的值．
解答：∵a+b=3，
∴（a+b）2=a2+2ab+b2=9，
∴a2+b2=9-2ab，
∵a3+b3=（a+b）（a2-ab+b2）=（a+b）[（a+b）2-3ab）]=9，
∴ab=2．
故选B．
点评：主要考查了完全公式的应用．要注意完全平方公式：（a±b）2=a2±2ab+b2，对a3+b3的准确分解是解本题的关键．
分析：根据条件a+b=3，两边平方可求得a2+b2=9-2ab，再把条件a3+b3=9展成（a+b）和ab的形式，整体代入即可求得ab的值．
解答：∵a+b=3，
∴（a+b）2=a2+2ab+b2=9，
∴a2+b2=9-2ab，
∵a3+b3=（a+b）（a2-ab+b2）=（a+b）[（a+b）2-3ab）]=9，
∴ab=2．
故选B．
点评：主要考查了完全公式的应用．要注意完全平方公式：（a±b）2=a2±2ab+b2，对a3+b3的准确分解是解本题的关键．
练习册系列答案
相关题目
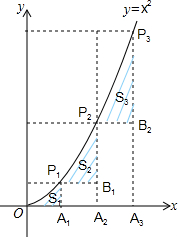如图，已知A1，A2，A3，…，A2012是x轴上的点，且0A1=A1A2=A2A3=…=A2010A2011=A2011A2012=1，分别过点A1，A2，A3，…，A2012作x轴的垂线交二次函数y=x2（x≥0）的图象于点P1，P2，P3，…，P2012，若△OA1P1的面积为S1，过点P1作P1B1⊥A2P2于点B1，记△P1B1P2的面积为S2，过点P2作P2B2⊥A3P3于点B2，记△P2B2P3的面积为S3，…依次进行下去，最后记△P2011B2011P2012的面积为S20121，则