题目内容
8、已知a1，a2，a3，a4，a5是满足条件a1+a2+a3+a4+a5=9的五个不同的整数，若b是关于x的方程（x-a1）（x-a2）（x-a3）（x-a4）（x-a5）=2009的整数根，则b的值为
10
．分析：先根据已知条件可知b-a1，b-a2，b-a3，b-a4，b-a5是五个不同的整数，再把2009分解成五个整数积的形式，再把五个整数相加即可求出b-a1+b-a2+b-a3+b-a4+b-a5的值，在与a1+a2+a3+a4+a5=9联立即可求解．
解答：解：因为（b-a1）（b-a2）（b-a3）（b-a4）（b-a5）=2009，
且a1，a2，a3，a4，a5是五个不同的整数，
所有b-a1，b-a2，b-a3，b-a4，b-a5也是五个不同的整数．
又因为2009=1×（-1）×7×（-7）×41，
所以b-a1+b-a2+b-a3+b-a4+b-a5=41．
由a1+a2+a3+a4+a5=9，可得b=10．
故答案为：10．
且a1，a2，a3，a4，a5是五个不同的整数，
所有b-a1，b-a2，b-a3，b-a4，b-a5也是五个不同的整数．
又因为2009=1×（-1）×7×（-7）×41，
所以b-a1+b-a2+b-a3+b-a4+b-a5=41．
由a1+a2+a3+a4+a5=9，可得b=10．
故答案为：10．
点评：本题考查的是方程的整数根问题，根据题意把2009分解成几个整数积的形式是解答此题的关键．
练习册系列答案
相关题目
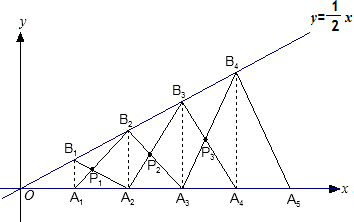
如图，已知A1，A2，A3，…，A2006是x轴上的点，且OA1=A1A2=A2A3=…=A2005A2006=1，分别过点A1，A2，A3，…，A2006作x轴的垂线交二次函数y=x2（x≥0）的图象于点P1，P2，P3，…，P2006点，若记△OA1P1的面积为S1，过点P1作P1B1⊥A2P2于点B1，记△P1B1P2的面积为S2，过点P2作P2B2⊥A3P3于点B2，记△P2B2P3的面积为S3，…，依次进行下去，最后记△P2005B2005P2006的面积为S2006，则S2006-S2005=