题目内容
 如图,已知A1,A2,A3,…,A2012是x轴上的点,且0A1=A1A2=A2A3=…=A2010A2011=A2011A2012=1,分别过点A1,A2,A3,…,A2012作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2012,若△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2011B2011P2012的面积为S20121,则
如图,已知A1,A2,A3,…,A2012是x轴上的点,且0A1=A1A2=A2A3=…=A2010A2011=A2011A2012=1,分别过点A1,A2,A3,…,A2012作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2012,若△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2011B2011P2012的面积为S20121,则| s1+s2+s3+…+s2012 |
分析:解答这道题,需要找出S1、S2、S3、…Sn之间的关系,通过图示可以发现:0A1=A1A2=A2A3=…=A2010A2011=A2011A2012=1,即这些直角三角形的一条直角边是相等的,所以只需找出它们的另一条直角边之间的关系即可;P1A1=12=2-1、P2B1=22-12=2×2-1、P3B2=32-22=5=2×3-1、…、PnBn-1=n2-(n-1)2=2n-1,所以在解答
时,只需应用一次等差数列的前n项和即可.
| s1+s2+s3+…+s2012 |
解答:解:∵0A1=A1A2=A2A3=…=A2010A2011=A2011A2012=1,
即:A1(1,0)、A2(2,0)、A3(3,0)、…An(n,0),
∴P1A1=12=2-1
P2B1=22-12=2×2-1
P3B2=32-22=5=2×3-1
…
PnBn-1=n2-(n-1)2=2n-1
∴
=
=
=1006
故选C.
即:A1(1,0)、A2(2,0)、A3(3,0)、…An(n,0),
∴P1A1=12=2-1
P2B1=22-12=2×2-1
P3B2=32-22=5=2×3-1
…
PnBn-1=n2-(n-1)2=2n-1
∴
| s1+s2+s3+…+s2012 |
|
|
| 2 |
故选C.
点评:考查了二次函数综合题.解答此类规律型题目,关键是找出问题中的规律,在此题中,找出各直角三角形高之间的关系是解答题目的关键.另外,等差数列前n项的求和公式(Sn=
)需要牢记.
| (a1+an)n |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

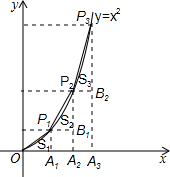 如图,已知A1,A2,A3,…,A2009是x轴上的点,且OA1=A1A2=A2A3=…=A2008A2009=1,分别过点A1,A2,A3,…,A2009作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2009,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…,依次进行下去,最后记△P2008B2008P2009的面积为S2009,则S2009-S2008=
如图,已知A1,A2,A3,…,A2009是x轴上的点,且OA1=A1A2=A2A3=…=A2008A2009=1,分别过点A1,A2,A3,…,A2009作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2009,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…,依次进行下去,最后记△P2008B2008P2009的面积为S2009,则S2009-S2008= 如图,已知A1,A2,A3,…,A2006是x轴上的点,且OA1=A1A2=A2A3=…=A2005A2006=1,分别过点A1,A2,A3,…,A2006作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2006点,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…,依次进行下去,最后记△P2005B2005P2006的面积为S2006,则S2006-S2005=
如图,已知A1,A2,A3,…,A2006是x轴上的点,且OA1=A1A2=A2A3=…=A2005A2006=1,分别过点A1,A2,A3,…,A2006作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2006点,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…,依次进行下去,最后记△P2005B2005P2006的面积为S2006,则S2006-S2005=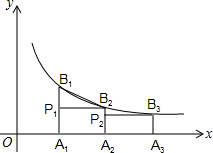 如图,已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…An作x轴的垂线交反比例函数y=
如图,已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…An作x轴的垂线交反比例函数y=