题目内容
28、已知a1、a2、a3、a4、a5为非负有理数，且M=（a1+a2+a3+a4）（a2+a3+a4+a5），N=（a1+a2+a3+a4+a5）（a2+a3+a4），试比较M、N的大小．
分析：运用多项式的乘法先计算，再比较大小．
解答：解：∵M=（a1+a2+a3+a4）（a2+a3+a4+a5）=（a1+a2+a3+a4）（a2+a3+a4）+a5（a1+a2+a3+a4），
N=（a1+a2+a3+a4+a5）（a2+a3+a4）=（a1+a2+a3+a4）（a2+a3+a4）+a5（a2+a3+a4），
∴M-N=a5（a1+a2+a3+a4）-a5（a2+a3+a4）=a5•a1，
又已知a1、a2、a3、a4、a5为非负有理数，
∴M≥N．
N=（a1+a2+a3+a4+a5）（a2+a3+a4）=（a1+a2+a3+a4）（a2+a3+a4）+a5（a2+a3+a4），
∴M-N=a5（a1+a2+a3+a4）-a5（a2+a3+a4）=a5•a1，
又已知a1、a2、a3、a4、a5为非负有理数，
∴M≥N．
点评：本题考查了多项式的乘法，熟练掌握运算法则并灵活运用是解题的关键，求差法是比较大小的常用方法之一．
练习册系列答案
名校课堂系列答案
相关题目
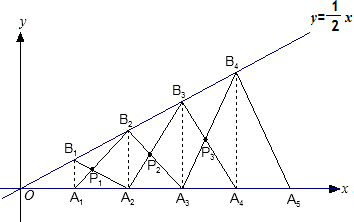
如图，已知A1，A2，A3，…，A2006是x轴上的点，且OA1=A1A2=A2A3=…=A2005A2006=1，分别过点A1，A2，A3，…，A2006作x轴的垂线交二次函数y=x2（x≥0）的图象于点P1，P2，P3，…，P2006点，若记△OA1P1的面积为S1，过点P1作P1B1⊥A2P2于点B1，记△P1B1P2的面积为S2，过点P2作P2B2⊥A3P3于点B2，记△P2B2P3的面积为S3，…，依次进行下去，最后记△P2005B2005P2006的面积为S2006，则S2006-S2005=