ЬтФПФкШн
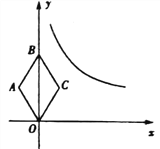
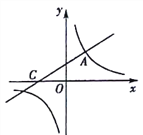
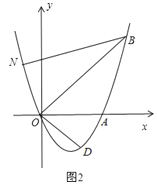
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯпy=ax2+bxЃЈaЁй0ЃЉОЙ§AЃЈ6ЃЌ0ЃЉЁЂBЃЈ8ЃЌ8ЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉНЋжБЯпOBЯђЯТЦНвЦmИіЕЅЮЛГЄЖШКѓЃЌЕУЕНЕФжБЯпгыХзЮяЯпжЛгавЛИіЙЋЙВЕуDЃЌЧѓmЕФжЕМАЕуDЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуNдкХзЮяЯпЩЯЃЌЧвЁЯNBO=ЁЯABOЃЌдђдкЃЈ2ЃЉЕФЬѕМўЯТЃЌдкзјБъЦНУцФкгаЕуPЃЌЧѓГіЫљгаТњзуЁїPODЁзЁїNOBЕФЕуPзјБъЃЈЕуPЁЂOЁЂDЗжБ№гыЕуNЁЂOЁЂBЖдгІЃЉЃЎ
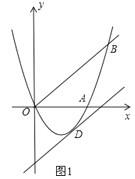
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЪЧy=![]() x2Љ3xЃЛЃЈ2ЃЉDЕуЕФзјБъЮЊЃЈ4ЃЌЉ4ЃЉЃЛЃЈ3ЃЉЕуPЕФзјБъЪЧЃЈ
x2Љ3xЃЛЃЈ2ЃЉDЕуЕФзјБъЮЊЃЈ4ЃЌЉ4ЃЉЃЛЃЈ3ЃЉЕуPЕФзјБъЪЧЃЈ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪННјЖјЕУГіД№АИМДПЩЃЛ
ЃЈ2ЃЉЪзЯШЧѓГіжБЯпOBЕФНтЮіЪНЮЊy=xЃЌНјЖјНЋЖўДЮКЏЪ§вдвЛДЮКЏЪ§СЊСЂЧѓГіНЛЕуМДПЩЃЛ
ЃЈ3ЃЉЪзЯШЧѓГіжБЯпAЁфBЕФНтЮіЪНЃЌНјЖјгЩЁїP1ODЁзЁїNOBЃЌЕУГіЁїP1ODЁзЁїN1OB1ЃЌНјЖјЧѓГіЕуP1ЕФзјБъЃЌдйРћгУЗелБфЛЛЕФаджЪЕУГіСэвЛЕуЕФзјБъЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉЁпХзЮяЯпy=ax2+bxЃЈaЁй0ЃЉОЙ§AЃЈ6ЃЌ0ЃЉЁЂBЃЈ8ЃЌ8ЃЉ
ЁрНЋAгыBСНЕузјБъДњШыЕУЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЪЧy=![]() x2Љ3xЃЎ
x2Љ3xЃЎ
ЃЈ2ЃЉЩшжБЯпOBЕФНтЮіЪНЮЊy=k1xЃЌгЩЕуBЃЈ8ЃЌ8ЃЉЃЌ
ЕУЃК8=8k1ЃЌНтЕУЃКk1=1
ЁржБЯпOBЕФНтЮіЪНЮЊy=xЃЌ
ЁржБЯпOBЯђЯТЦНвЦmИіЕЅЮЛГЄЖШКѓЕФНтЮіЪНЮЊЃКy=xЉmЃЌ
ЁрxЉm=![]() x2Љ3xЃЌ
x2Љ3xЃЌ
ЁпХзЮяЯпгыжБЯпжЛгавЛИіЙЋЙВЕуЃЌ
ЁрЁї=16Љ2m=0ЃЌ
НтЕУЃКm=8ЃЌ
ДЫЪБx1=x2=4ЃЌy=x2Љ3x=Љ4ЃЌ
ЁрDЕуЕФзјБъЮЊЃЈ4ЃЌЉ4ЃЉ
ЃЈ3ЃЉЁпжБЯпOBЕФНтЮіЪНЮЊy=xЃЌЧвAЃЈ6ЃЌ0ЃЉЃЌ
ЁрЕуAЙигкжБЯпOBЕФЖдГЦЕуAЁфЕФзјБъЪЧЃЈ0ЃЌ6ЃЉЃЌ
ИљОнжсЖдГЦаджЪКЭШ§ЯпКЯвЛаджЪЕУГіЁЯAЁфBO=ЁЯABOЃЌ
ЩшжБЯпAЁфBЕФНтЮіЪНЮЊy=k2x+6ЃЌЙ§ЕуЃЈ8ЃЌ8ЃЉЃЌ
Ёр8k2+6=8ЃЌНтЕУЃКk2=![]() ЃЌ
ЃЌ
ЁржБЯпAЁфBЕФНтЮіЪНЪЧy=![]() ЃЌ
ЃЌ
ЁпЁЯNBO=ЁЯABOЃЌЁЯAЁфBO=ЁЯABOЃЌ
ЁрBAЁфКЭBNжиКЯЃЌМДЕуNдкжБЯпAЁфBЩЯЃЌ
ЁрЩшЕуNЃЈnЃЌ![]() ЃЉЃЌгжЕуNдкХзЮяЯпy=
ЃЉЃЌгжЕуNдкХзЮяЯпy=![]() x2Љ3xЩЯЃЌ
x2Љ3xЩЯЃЌ
Ёр![]() =
=![]() n2Љ3nЃЌ НтЕУЃКn1=Љ
n2Љ3nЃЌ НтЕУЃКn1=Љ![]() ЃЌn2=8ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉ
ЃЌn2=8ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉ
ШчЭМ1ЃЌНЋЁїNOBбиxжсЗелЃЌЕУЕНЁїN1OB1ЃЌ

дђN1ЃЈЉ![]() ЃЌ-
ЃЌ-![]() ЃЉЃЌB1ЃЈ8ЃЌЉ8ЃЉЃЌ
ЃЉЃЌB1ЃЈ8ЃЌЉ8ЃЉЃЌ
ЁрOЁЂDЁЂB1ЖМдкжБЯпy=ЉxЩЯЃЎ
ЁпЁїP1ODЁзЁїNOBЃЌЁїNOBЁеЁїN1OB1ЃЌ
ЁрЁїP1ODЁзЁїN1OB1ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕуP1ЕФзјБъЮЊЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
НЋЁїOP1DбижБЯпy=ЉxЗелЃЌПЩЕУСэвЛИіТњзуЬѕМўЕФЕуP2ЃЈ![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЫљЪіЃЌЕуPЕФзјБъЪЧЃЈ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЉЃЎ
ЃЉЃЎ

 УППЮБиСЗЯЕСаД№АИ
УППЮБиСЗЯЕСаД№АИ ЧЩбЇЧЩСЗЯЕСаД№АИ
ЧЩбЇЧЩСЗЯЕСаД№АИ