题目内容
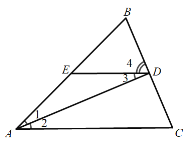
【题目】在△ABC中,AD平分∠BAC交BC于点D,在AB上取一点E,使得EA=ED.
(1)求证:DE∥AC;
(2)若ED=EB,BD=2,EA=3,求AD的长.

【答案】(1)见解析(2)4![]()
【解析】
(1)根据等腰三角形的性质即可求解;
(2)根据已知条件得到∠ADB=90°,再利用Rt△ABD中,由勾股定理即可求解.
(1)证明:∵AD平分∠BAC,
∴∠1=∠2.
∵EA=ED,
∴∠1=∠3.
∴∠2=∠3.
∴DE∥AC.
(2)∵ED=EB,ED=EA,
∴∠B=∠4,ED=EB=EA=3.
∴AB=6.
在△ABD中,∠B+∠4+∠3+∠1=180°,
∵∠1=∠3,∠B=∠4,
∴∠B+∠4+∠3+∠1=2∠3+2∠4=180°.
∴∠ADB=∠3+∠4=90°.
在Rt△ABD中,由勾股定理得:
![]()

练习册系列答案
相关题目
【题目】随机抽取某市一年(以365天计)中的30天的日平均气温状况统计如下:温度(![]() )
)
温度( | 10 | 14 | 18 | 22 | 26 | 30 | 32 |
天数 | 3 | 5 | 5 | 7 | 6 | 2 | 2 |
请根据上述数据回答下列问题:
(1)估计该城市年平均气温大约是多少?
(2)上表中的温度数据的中位数是_______众数是_________;
(3)计算该城市一年中约有几天的日平均气温为![]() ?
?